Date due funzioni ricorsive f e g. Ricorsione e algoritmi ricorsivi. Definizioni di base. Modi per rappresentare gli alberi
Per preparare gli studenti all'Esame di Stato Unificato di Informatica e ICT è stata realizzata una presentazione sul tema “Algoritmi Ricorsivi”. Il lavoro esamina la definizione di ricorsione e fornisce esempi di oggetti grafici definiti ricorsivamente. La presentazione contiene metodi per risolvere il compito n. 11 dalla bozza della versione demo dell'Esame di Stato Unificato - 2015 in informatica. Il primo metodo prevede la costruzione di un albero delle chiamate, il secondo metodo risolve il problema utilizzando il metodo di sostituzione. Vengono considerati 4 esempi di risoluzione di compiti utilizzando entrambi i metodi. La seguente presentazione contiene 25 esercizi per la formazione con risposte dal sito web di Konstantin Polyakov.
Scaricamento:
Anteprima:
Per utilizzare le anteprime delle presentazioni, crea un account Google e accedi ad esso: https://accounts.google.com
Didascalie delle diapositive:
Compito n. 11 Esame di stato unificato (livello base, tempo - 5 minuti) Algoritmi ricorsivi. Autore – Korotun O.V., insegnante di informatica, istituto scolastico municipale “Scuola secondaria n. 71”
Cosa devi sapere: La ricorsione è nella definizione, descrizione, rappresentazione di un oggetto o processo all'interno di questo oggetto o processo stesso, cioè una situazione in cui un oggetto è parte di se stesso. Lo stemma della Federazione Russa è un oggetto grafico definito ricorsivamente: nella zampa destra dell'aquila bicipite raffigurata su di esso è serrato uno scettro, che è coronato da una copia più piccola dello stemma. Poiché su questo stemma è presente anche uno scettro nella zampa destra dell'aquila, si ottiene una ricorsione infinita. Stemma ricorsivo della Russia
Nella programmazione, la ricorsione chiama una funzione da se stessa, direttamente o tramite altre funzioni, ad esempio, la funzione A chiama la funzione B e la funzione B chiama la funzione A. Il numero di chiamate annidate a una funzione o procedura è chiamato profondità della ricorsione. esempio di ricorsione: Se hai una macchia di grasso sul vestito, non preoccuparti. Le macchie di olio vengono rimosse con benzina. Le macchie di benzina vengono rimosse con una soluzione alcalina. Gli alcali vengono rimossi con l'essenza. Bene, sai già come rimuovere le macchie di olio.
Assegnazione di esempio: Dato un algoritmo ricorsivo: procedura F(n: intero); iniziare writeln(n); se n
Assegnazione di esempio: Dato un algoritmo ricorsivo: procedura F(n: intero); iniziare writeln(n) ; se n
Assegnazione di esempio: Dato un algoritmo ricorsivo: procedura F(n: intero); iniziare writeln(n); se n Diapositiva 9
Assegnazione di esempio: Dato un algoritmo ricorsivo: procedura F(n: intero); iniziare writeln(n); se n Diapositiva 10
Assegnazione di esempio: Dato un algoritmo ricorsivo: procedura F(n: intero); iniziare writeln(n); se n Diapositiva 11
15 Esempio n.2: Dato un algoritmo ricorsivo: procedura F(n: intero); iniziare writeln(n); se n
Esempio n.2: Dato un algoritmo ricorsivo: procedura F(n: intero); iniziare writeln(n); se n Diapositiva 13
Esempio n.3: Dato un algoritmo ricorsivo: procedura F(n: intero); iniziare writeln("*") ; se n > 0 allora inizia F(n-2); F(n div 2) fine fine ; Quanti asterischi verranno stampati sullo schermo quando si chiama F(7)? 7 5 3 2 3 1 1 1 1 In questo esempio sullo schermo viene visualizzato il simbolo * -2 div 2 1 0 -1 0 -1 0 -1 -1 -1 0 0 0 anziché i valori del parametro n.
Esempio n.3: Dato un algoritmo ricorsivo: procedura F(n: intero); iniziare writeln("*"); se n > 0 allora inizia F(n-2); F(n div 2) fine fine ; Quanti asterischi verranno stampati sullo schermo quando si chiama F(7)? * Contando il numero di “stelle” otteniamo 21. In questo esempio sullo schermo non vengono visualizzati i valori del parametro n, ma il simbolo * * * * * * * * * * * * * * * * * * * * * *
Esempio n.3: Dato un algoritmo ricorsivo: procedura F(n: intero); iniziare writeln("*"); se n > 0 allora inizia F(n-2); F(n div 2) fine fine ; Quanti asterischi verranno stampati sullo schermo quando si chiama F(7)? Risolviamo il problema senza un albero. Sia S(n) il numero di “stelle” che verranno stampate quando si chiama F(n). Allora 1+S(n-2)+ S(n div 2), n>0 1 , n Dobbiamo conoscere S(7). S(7)= 1 +S(5)+ S(3) S(5)= 1 +S(3)+S(2) S(3)= 1 +S(1)+S(1) S( 2)=1+S(0)+S(1)=1+1+S(1)=2+S(1) S(1)= 1+ S(-1)+S(0)=1+ 1+1=3 Inverso: S(2)=2+3=5 S(3)=1+3+3=7 S(5)=1+7+5=13 S(7)=1+ 13+ 7= 21 S(n)=
Esempio n.4: procedura F(n: intero); iniziare se n Diapositiva 18
Esempio n.4: procedura F(n: intero); iniziare se n Diapositiva 19
Esempio n.4: procedura F(n: intero); iniziare se n
Esempio n.4: procedura F(n: intero); iniziare se n
Compiti di formazione
Problema 1: Dato un algoritmo ricorsivo: procedura F(n: intero); iniziare writeln("*"); se n > 0 allora inizia F(n-2); F(ndiv2); F(ndiv2); fine fine; Quanti asterischi verranno stampati sullo schermo quando si chiama F(5)? Risposta: 34
Problema 2: Dato un algoritmo ricorsivo: procedura F(n: intero); iniziare writeln("*"); se n > 0 allora inizia F(n-2); F(n-2); F(ndiv2); fine fine; Quanti asterischi verranno stampati sullo schermo quando si chiama F(6)? Risposta: 58
Problema 3: Dato un algoritmo ricorsivo: procedura F(n: intero); iniziare writeln("*"); se n > 0 allora inizia F(n-3); F(ndiv2); fine fine; Quanti asterischi verranno stampati sullo schermo quando si chiama F(7)? Risposta: 15
Problema 4: Dato un algoritmo ricorsivo: procedura F(n: intero); iniziare writeln("*"); se n > 0 allora inizia F(n-3); F(n-2); F(ndiv2); fine fine; Quanti asterischi verranno stampati sullo schermo quando si chiama F(7)? Risposta: 55
Problema 5: Dato un algoritmo ricorsivo: procedura F(n: intero); iniziare writeln("*"); se n > 0 allora inizia F(n-3); F(n-2); F(ndiv2); F(ndiv2); fine fine; Quanti asterischi verranno stampati sullo schermo quando si chiama F(6)? Risposta: 97
Problema 6: Dato un algoritmo ricorsivo: procedura F(n: intero); iniziare writeln("*"); se n > 0 allora inizia writeln("*"); F(n-2); F(ndiv2); fine fine; Quanti asterischi verranno stampati sullo schermo quando si chiama F(7)? Risposta: 31
Problema 7: Dato un algoritmo ricorsivo: procedura F(n: intero); iniziare writeln("*"); se n > 0 allora inizia writeln("*"); F(n-2); F(ndiv2); F(ndiv2); fine fine; Quanti asterischi verranno stampati sullo schermo quando si chiama F(7)? Risposta: 81
Problema 8: Dato un algoritmo ricorsivo: procedura F(n: intero); iniziare writeln("*"); se n > 0 allora inizia writeln("*"); F(n-2); F(n-2); F(ndiv2); fine fine; Quanti asterischi verranno stampati sullo schermo quando si chiama F(6)? Risposta: 77
Problema 9: Dato un algoritmo ricorsivo: procedura F(n: intero); inizia se n > 0 allora inizia F(n-2); F(n-1); F(n-1); FINE; writeln("*"); FINE ; Quanti asterischi verranno stampati sullo schermo quando si chiama F(5)? Risposta: 148
Problema 10: Dato un algoritmo ricorsivo: procedura F(n: intero); comincia se n > 0 allora comincia writeln("*"); F(n-2); F(n-1); F(n-1); FINE; writeln("*"); FINE; Quanti asterischi verranno stampati sullo schermo quando si chiama F(5)? Risposta: 197
Problema 11: Dato un algoritmo ricorsivo: procedura F(n: intero); iniziare se n > 1 allora iniziare F(n-2); F(n-1); F(ndiv2); FINE; writeln("*"); FINE ; Quanti asterischi verranno stampati sullo schermo quando si chiama F(7)? Risposta: 88
Problema 12: Dato un algoritmo ricorsivo: procedura F(n: intero); comincia se n > 2 allora comincia writeln("*"); F(n-2); F(n-1); F(ndiv2); FINE ; writeln("*"); FINE; Quanti asterischi verranno stampati sullo schermo quando si chiama F(6)? Risposta: 33
Problema 13: Dato un algoritmo ricorsivo: procedura F (n: intero); iniziare writeln(n); se n
Problema 14: Dato un algoritmo ricorsivo: procedura F (n: intero); iniziare writeln(n); se n
Problema 15: Dato un algoritmo ricorsivo: procedura F (n: intero); iniziare writeln(n); se n
Problema 16: Dato un algoritmo ricorsivo: procedura F (n: intero); iniziare writeln(n); se n
Problema 17: Dato un algoritmo ricorsivo: procedura F (n: intero); iniziare writeln(n); se n
Problema 18: Dato un algoritmo ricorsivo: procedura F (n: intero); iniziare writeln(n); se n
Problema 19: Dato un algoritmo ricorsivo: procedura F (n: intero); iniziare writeln(n); se n
Problema 20: Dato un algoritmo ricorsivo: procedura F (n: intero); iniziare writeln(n); se n
Problema 21: Dato un algoritmo ricorsivo: procedura F (n: intero); iniziare writeln(n); se n
Problema 22: Dato un algoritmo ricorsivo: procedura F (n: intero); iniziare writeln(n); se n
Problema 23: Dato un algoritmo ricorsivo: procedura F (n: intero); iniziare writeln(n); se n
Problema 24: Dato un algoritmo ricorsivo: procedura F (n: intero); iniziare writeln(n); se n
Problema 25: Dato un algoritmo ricorsivo: procedura F (n: intero); iniziare writeln(n); se n
La ricorsione avviene quando una subroutine richiama se stessa. Di fronte a un progetto algoritmico di questo tipo per la prima volta, la maggior parte delle persone incontra alcune difficoltà, ma con un po' di pratica, la ricorsione diventerà uno strumento comprensibile e molto utile nel proprio arsenale di programmazione.
1. L'essenza della ricorsione
Una procedura o funzione può contenere chiamate ad altre procedure o funzioni. La procedura può anche richiamare se stessa. Non c'è alcun paradosso qui: il computer esegue solo in sequenza i comandi che incontra nel programma e, se incontra una chiamata di procedura, inizia semplicemente a eseguire questa procedura. Non importa quale procedura abbia dato il comando per farlo.
Esempio di procedura ricorsiva:
Procedura Rec(a: intero); iniziare se a>
Consideriamo cosa succede se nel programma principale viene effettuata una chiamata, ad esempio, della forma Rec(3). Di seguito è riportato un diagramma di flusso che mostra la sequenza di esecuzione delle istruzioni.
Riso. 1. Schema a blocchi della procedura ricorsiva.
La procedura Rec viene chiamata con parametro a = 3. Contiene una chiamata alla procedura Rec con parametro a = 2. La chiamata precedente non è ancora stata completata, quindi puoi immaginare che viene creata un'altra procedura e la prima non termina il suo lavoro fino a quando finisce. Il processo chiamante termina quando il parametro a = 0. A questo punto vengono eseguite contemporaneamente 4 istanze della procedura. Viene chiamato il numero di procedure eseguite simultaneamente profondità di ricorsione.
La quarta procedura chiamata (Rec(0)) stamperà il numero 0 e finirà il suo lavoro. Successivamente, il controllo ritorna alla procedura che lo ha chiamato (Rec(1)) e viene stampato il numero 1 E così via fino al completamento di tutte le procedure. La chiamata originale stamperà quattro numeri: 0, 1, 2, 3.
Un'altra immagine visiva di ciò che sta accadendo è mostrata in Fig. 2.

Riso. 2. Eseguire la procedura Rec con parametro 3 consiste nell'eseguire la procedura Rec con parametro 2 e stampare il numero 3. A sua volta eseguire la procedura Rec con parametro 2 consiste nell'eseguire la procedura Rec con parametro 1 e stampare il numero 2. Ecc .
Come esercizio, considera cosa succede quando chiami Rec(4). Considera anche cosa accadrebbe se chiamassi la procedura Rec2(4) di seguito, con gli operatori invertiti.
Procedura Rec2(a: intero); iniziare writeln(a); se a>0 allora Rec2(a-1); FINE;
Tieni presente che in questi esempi la chiamata ricorsiva è all'interno di un'istruzione condizionale. Questa è una condizione necessaria affinché la ricorsione abbia mai fine. Da notare inoltre che la procedura richiama se stessa con un parametro diverso da quello con cui è stata richiamata. Se la procedura non utilizza variabili globali, ciò è necessario affinché la ricorsione non continui all'infinito.
È possibile uno schema leggermente più complesso: la funzione A chiama la funzione B, che a sua volta chiama A. Questa viene chiamata ricorsione complessa. Si scopre che la procedura descritta per prima deve richiamare una procedura che non è stata ancora descritta. Affinché ciò sia possibile, è necessario utilizzare .
Procedura A(n: intero); (Descrizione in avanti (intestazione) della prima procedura) procedura B(n: intero); (Descrizione successiva della seconda procedura) procedura A(n: intero); (Descrizione completa della procedura A) Begin writeln(n); B(n-1); FINE; procedura B(n: intero); (Descrizione completa della procedura B) Begin writeln(n); se n
La dichiarazione anticipata della procedura B consente di richiamarla dalla procedura A. La dichiarazione anticipata della procedura A non è richiesta in questo esempio e viene aggiunta per ragioni estetiche.
Se la ricorsione ordinaria può essere paragonata a un ouroboros (Fig. 3), allora l'immagine della ricorsione complessa può essere tratta dalla famosa poesia per bambini, dove "I lupi si spaventarono e si mangiarono a vicenda". Immagina due lupi che si mangiano a vicenda e capirai la ricorsione complessa.

Riso. 3. Ouroboros - un serpente che divora la propria coda. Tratto dal trattato alchemico “Synosius” di Theodore Pelecanos (1478).

Riso. 4. Ricorsione complessa.
3. Simulare un ciclo utilizzando la ricorsione
Se una procedura richiama se stessa, essenzialmente fa sì che le istruzioni in essa contenute vengano eseguite nuovamente, in modo simile a un ciclo. Alcuni linguaggi di programmazione non contengono affatto costrutti di loop, lasciando ai programmatori il compito di organizzare le ripetizioni utilizzando la ricorsione (ad esempio Prolog, dove la ricorsione è una tecnica di programmazione di base).
Ad esempio, simuliamo il funzionamento di un ciclo for. Per fare ciò abbiamo bisogno di una variabile contapassi, che può essere implementata ad esempio come parametro di procedura.
Esempio 1.
Procedura LoopImitation(i, n: intero); (Il primo parametro è il contapassi, il secondo parametro è il numero totale di passi) Begin writeln("Ciao N ", i); //Ecco tutte le istruzioni che verranno ripetute se i Il risultato di una chiamata nella forma LoopImitation(1, 10) sarà l'esecuzione delle istruzioni dieci volte, modificando il contatore da 1 a 10. In questo caso verrà stampato quanto segue: Ciao N1 In generale, non è difficile vedere che i parametri della procedura sono i limiti per modificare i valori del contatore. È possibile scambiare la chiamata ricorsiva e le istruzioni da ripetere, come nell'esempio seguente. Esempio 2.
Procedura LoopImitation2(i, n: intero); iniziare se i In questo caso, si verificherà una chiamata di procedura ricorsiva prima che le istruzioni inizino ad essere eseguite. Anche la nuova istanza della procedura chiamerà innanzitutto un'altra istanza e così via, fino a raggiungere il valore massimo del contatore. Solo dopo l'ultima delle procedure richiamate eseguirà le sue istruzioni, poi la penultima eseguirà le sue istruzioni, ecc. Il risultato della chiamata a LoopImitation2(1, 10) sarà la stampa dei saluti in ordine inverso: Ciao N10 Se immaginiamo una catena di procedure chiamate ricorsivamente, nell'esempio 1 la percorriamo dalle procedure chiamate in precedenza a quelle successive. Nell'esempio 2, al contrario, da dopo a prima. Infine, è possibile inserire una chiamata ricorsiva tra due blocchi di istruzioni. Per esempio: Procedura LoopImitation3(i, n: intero); Begin writeln("Ciao N ", i); (Il primo blocco di istruzioni potrebbe trovarsi qui) se i Qui le istruzioni del primo blocco vengono prima eseguite in sequenza, poi le istruzioni del secondo blocco vengono eseguite in ordine inverso. Quando chiamiamo LoopImitation3(1, 10) otteniamo: Ciao N1 Ci vorrebbero due cicli per fare la stessa cosa senza ricorsione. Puoi trarre vantaggio dal fatto che l'esecuzione di parti di una stessa procedura è distanziata nel tempo. Per esempio: Esempio 3: conversione di un numero in binario.
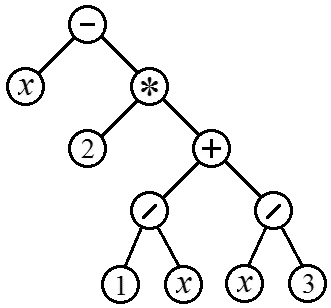
Ottenere le cifre di un numero binario, come è noto, avviene dividendo con un resto per la base del sistema numerico 2. Se c'è un numero, la sua ultima cifra nella sua rappresentazione binaria è uguale a Prendendo l'intera parte della divisione per 2: otteniamo un numero che ha la stessa rappresentazione binaria, ma senza l'ultima cifra. Pertanto, è sufficiente ripetere le due operazioni precedenti finché il campo di divisione successivo non riceve una parte intera uguale a 0. Senza ricorsione sarà simile a questo: Mentre x>0 inizia c:=x mod 2; x:=xdiv2; scrivere(c); FINE; Il problema qui è che le cifre della rappresentazione binaria vengono calcolate in ordine inverso (prima la più recente). Per stampare un numero in forma normale, dovrai ricordare tutti i numeri negli elementi dell'array e stamparli in un ciclo separato. Usando la ricorsione, non è difficile ottenere l'output nell'ordine corretto senza un array e un secondo ciclo. Vale a dire: Procedura Rappresentazione binaria(x: intero); var c, x: intero; Begin (Primo blocco. Eseguito in ordine di chiamate di procedura) c:= x mod 2; x:= xdiv2; (Chiamata ricorsiva) se x>0 allora BinaryRepresentation(x); (Secondo blocco. Eseguito in ordine inverso) write(c); FINE; In generale non abbiamo ricevuto alcuna vincita. Le cifre della rappresentazione binaria sono memorizzate in variabili locali, che sono diverse per ogni istanza in esecuzione della procedura ricorsiva. Cioè, non è stato possibile salvare la memoria. Al contrario, sprechiamo memoria extra memorizzando molte variabili locali x. Comunque questa soluzione mi sembra bellissima. Una sequenza di vettori si dice data da una relazione ricorsiva se sono dati il vettore iniziale e la dipendenza funzionale del vettore successivo dal precedente Un semplice esempio di quantità calcolata utilizzando le relazioni di ricorrenza è il fattoriale Il fattoriale successivo può essere calcolato dal precedente come: Introducendo la notazione , otteniamo la relazione: I vettori della formula (1) possono essere interpretati come insiemi di valori variabili. Quindi il calcolo dell'elemento richiesto della sequenza consisterà nel ripetuto aggiornamento dei loro valori. In particolare per il fattoriale: X:= 1; per i:= 2 to n fare x:= x * i; scriviln(x); Viene chiamato ciascuno di questi aggiornamenti (x:= x * i). iterazione, e il processo di ripetizione delle iterazioni è iterazione. Notiamo però che la relazione (1) è una definizione puramente ricorsiva della sequenza e il calcolo dell'ennesimo elemento è in realtà il ripetuto prelievo della funzione f da se stessa: In particolare, per il fattoriale si può scrivere: Funzione Fattoriale(n: intero): intero; comincia se n > 1 allora Fattoriale:= n * Fattoriale(n-1) else Fattoriale:= 1; FINE; Dovrebbe essere chiaro che la chiamata di funzioni comporta un sovraccarico aggiuntivo, quindi la prima opzione per il calcolo del fattoriale sarà leggermente più veloce. In generale, le soluzioni iterative funzionano più velocemente di quelle ricorsive. Prima di passare alle situazioni in cui la ricorsione è utile, esaminiamo un altro esempio in cui non dovrebbe essere utilizzata. Consideriamo un caso speciale di relazioni ricorrenti, quando il valore successivo nella sequenza dipende non da uno, ma da più valori precedenti contemporaneamente. Un esempio è la famosa sequenza di Fibonacci, in cui ogni elemento successivo è la somma dei due precedenti: Con un approccio “frontale” si può scrivere: Funzione Fib(n: intero): intero; iniziare se n > 1 allora Fib:= Fib(n-1) + Fib(n-2) altrimenti Fib:= 1; FINE; Ogni chiamata Fib crea due copie di se stessa, ogni copia ne crea altre due e così via. Il numero di operazioni aumenta con il numero N esponenzialmente, anche se con una soluzione iterativa lineare N numero di operazioni. In effetti, l’esempio sopra ci insegna il contrario QUANDO la ricorsione non dovrebbe essere utilizzata, altrimenti COME non dovrebbe essere usato. Dopotutto, se esiste una soluzione iterativa veloce (basata su loop), lo stesso loop può essere implementato utilizzando una procedura o una funzione ricorsiva. Per esempio: // x1, x2 – condizioni iniziali (1, 1) // n – numero della funzione del numero di Fibonacci richiesta Fib(x1, x2, n: intero): intero; var x3: intero; inizia se n > 1 allora inizia x3:= x2 + x1; x1:=x2; x2:=x3; Fib:= Fib(x1, x2, n-1); fine altrimenti Fib:= x2; FINE; Tuttavia, sono preferibili soluzioni iterative. La domanda è: quando dovrebbe essere utilizzata la ricorsione in questo caso? Qualsiasi procedura e funzione ricorsiva che contenga una sola chiamata ricorsiva a se stessa può essere facilmente sostituita da cicli iterativi. Per ottenere qualcosa che non abbia una controparte semplice e non ricorsiva è necessario ricorrere a procedure e funzioni che si richiamano due o più volte. In questo caso l’insieme delle procedure richiamate non forma più una catena, come in Fig. 1, ma un intero albero. Esistono ampie classi di problemi in cui il processo computazionale deve essere organizzato in questo modo. Per loro, la ricorsione sarà la soluzione più semplice e naturale. La base teorica per le funzioni ricorsive che si chiamano più di una volta è la branca della matematica discreta che studia gli alberi. Definizione:
chiameremo insieme finito T, costituito da uno o più nodi tali che: Questa definizione è ricorsiva. In breve, un albero è un insieme costituito da una radice e da sottoalberi ad essa collegati, che sono anche alberi. Un albero è definito attraverso se stesso. Tuttavia, questa definizione ha senso perché la ricorsione è finita. Ogni sottoalbero contiene meno nodi dell'albero che lo contiene. Alla fine arriviamo a sottoalberi contenenti un solo nodo, e questo è già chiaro di cosa si tratta. Riso. 3. Albero. Nella fig. La Figura 3 mostra un albero con sette nodi. Sebbene gli alberi normali crescano dal basso verso l'alto, è consuetudine disegnarli al contrario. Quando si disegna un diagramma a mano, questo metodo è ovviamente più conveniente. A causa di questa incoerenza, a volte sorge confusione quando si dice che un nodo è sopra o sotto un altro. Per questo motivo è più conveniente utilizzare la terminologia utilizzata per descrivere gli alberi genealogici, chiamando i nodi più vicini agli antenati radice e quelli più distanti discendenti. Un albero può essere rappresentato graficamente in altri modi. Alcuni di essi sono mostrati in Fig. 4. Secondo la definizione, un albero è un sistema di insiemi nidificati, dove questi insiemi non si intersecano o sono completamente contenuti l'uno nell'altro. Tali insiemi possono essere rappresentati come regioni su un piano (Fig. 4a). Nella fig. 4b, gli insiemi nidificati non si trovano su un piano, ma sono allungati in un'unica linea. Riso. 4b può anche essere visto come un diagramma di una formula algebrica contenente parentesi annidate. Riso. La Figura 4c fornisce un altro modo popolare di rappresentare una struttura ad albero come un elenco sfalsato. Riso. 4. Altri modi per rappresentare strutture ad albero: (a) insiemi nidificati; (b) parentesi annidate; c) elenco delle concessioni. L'elenco sfalsato presenta evidenti somiglianze con il modo in cui viene formattato il codice del programma. Infatti, un programma scritto nell'ambito del paradigma di programmazione strutturata può essere rappresentato come un albero costituito da strutture annidate. Puoi anche tracciare un'analogia tra l'elenco a gradini e l'aspetto dei sommari nei libri, dove le sezioni contengono sottosezioni, che a loro volta contengono sottosezioni, ecc. Il modo tradizionale di numerare tali sezioni (sezione 1, sottosezioni 1.1 e 1.2, sottosezione 1.1.2, ecc.) è chiamato sistema decimale Dewey. Applicato all'albero di Fig. 3 e 4 questo sistema darà: 1.A; 1.1B; 1,2 C; 1.2.1D; 1.2.2 E; 1.2.3 F; 1.2.3.1 G; In tutti gli algoritmi relativi alle strutture ad albero appare invariabilmente la stessa idea, vale a dire l'idea passando O attraversamento degli alberi. Questo è un modo di visitare i nodi dell'albero in cui ciascun nodo viene attraversato esattamente una volta. Ciò si traduce in una disposizione lineare dei nodi dell'albero. In particolare, ci sono tre modi: puoi percorrere i nodi in ordine avanti, indietro e finale. Algoritmo di attraversamento in avanti: Questo algoritmo è ricorsivo, poiché l'attraversamento di un albero contiene l'attraversamento di sottoalberi e questi, a loro volta, vengono attraversati utilizzando lo stesso algoritmo. In particolare, per l'albero di Fig. 3 e 4, l'attraversamento diretto dà una sequenza di nodi: A, B, C, D, E, F, G. La sequenza risultante corrisponde a un'enumerazione dei nodi da sinistra a destra quando si rappresenta un albero utilizzando parentesi annidate e nella notazione decimale Dewey, nonché a un passaggio dall'alto verso il basso quando lo si rappresenta come un elenco sfalsato. Quando si implementa questo algoritmo in un linguaggio di programmazione, colpire la radice corrisponde alla procedura o alla funzione che esegue alcune azioni, e passare attraverso i sottoalberi corrisponde a chiamate ricorsive a se stessa. In particolare, per un albero binario (dove ogni nodo ha al massimo due sottoalberi), la procedura corrispondente sarebbe simile a questa: // Preorder Traversal – Nome inglese per la procedura di ordine diretto PreorderTraversal((Arguments)); inizio // Passando la radice DoSomething((Arguments)); //Transizione del sottoalbero sinistro se (esiste un sottoalbero sinistro) allora PreorderTransversal((Arguments 2)); //Transizione del sottoalbero destro se (esiste un sottoalbero destro) allora PreorderTransversal((Arguments 3)); FINE; Cioè, prima la procedura esegue tutte le azioni e solo dopo vengono eseguite tutte le chiamate ricorsive. Algoritmo di attraversamento inverso: Cioè, tutti i sottoalberi vengono attraversati da sinistra a destra e il ritorno alla radice si trova tra questi attraversamenti. Per l'albero di Fig. 3 e 4 si ottiene la sequenza dei nodi: B, A, D, C, E, G, F. In una corrispondente procedura ricorsiva, le azioni si troveranno negli spazi tra le chiamate ricorsive. Nello specifico per un albero binario: // Inorder Traversal – Nome inglese per la procedura di ordine inverso InorderTraversal((Arguments)); comincia // Percorre il sottoalbero sinistro se (esiste un sottoalbero sinistro) quindi InorderTraversal((Argomenti 2)); //Passando la root DoSomething((Arguments)); //Attraversa il sottoalbero destro se (esiste un sottoalbero destro) allora InorderTraversal((Argomenti 3)); FINE; Algoritmo di attraversamento dell'ordine finale: Per l'albero di Fig. 3 e 4 questo darà la sequenza dei nodi: B, D, E, G, F, C, A. In una procedura ricorsiva corrispondente, le azioni verranno posizionate dopo le chiamate ricorsive. Nello specifico per un albero binario: // Postorder Traversal – Nome inglese per la procedura dell'ordine finale PostorderTraversal((Arguments)); comincia // Viaggia nel sottoalbero sinistro se (c'è un sottoalbero sinistro) quindi PostorderTraversal((Argomenti 2)); //Trascendendo il sottoalbero destro se (esiste un sottoalbero destro) allora PostorderTraversal((Argomenti 3)); //Passando la root DoSomething((Arguments)); FINE; Se alcune informazioni si trovano nei nodi dell'albero, è possibile utilizzare un'appropriata struttura dati dinamica per memorizzarle. In Pascal, ciò viene fatto utilizzando una variabile di tipo record contenente puntatori a sottoalberi dello stesso tipo. Ad esempio, un albero binario in cui ciascun nodo contiene un numero intero può essere memorizzato utilizzando una variabile di tipo PTree, descritta di seguito: Digita PTree = ^TTree; TTree = record Inf: intero; LeftSubTree, RightSubTree: PTree; FINE; Ogni nodo ha un tipo PTree. Questo è un puntatore, il che significa che ogni nodo deve essere creato chiamando su di esso la procedura New. Se il nodo è un nodo foglia, il valore viene assegnato ai campi LeftSubTree e RightSubTree zero. In caso contrario, anche i nodi LeftSubTree e RightSubTree verranno creati dalla procedura New. Uno di questi record è mostrato schematicamente in Fig. 5. Riso. 5. Rappresentazione schematica di un record di tipo TTree. Il record ha tre campi: Inf – un numero, LeftSubTree e RightSubTree – puntatori a record dello stesso tipo TTree. Un esempio di albero composto da tali record è mostrato nella Figura 6. Riso. 6. Un albero composto da record di tipo TTree. Ciascuna voce memorizza un numero e due puntatori che possono contenerli zero o indirizzi di altri record dello stesso tipo. Se non hai mai lavorato in precedenza con strutture costituite da record contenenti collegamenti a record dello stesso tipo, ti consigliamo di familiarizzare con il materiale relativo. Consideriamo l'algoritmo per disegnare l'albero mostrato in Fig. 6. Se ogni linea è considerata un nodo, allora questa immagine soddisfa pienamente la definizione di albero data nella sezione precedente. Riso. 6. Albero. La procedura ricorsiva disegnerebbe ovviamente una linea (il tronco fino al primo ramo), per poi richiamarsi a disegnare i due sottoalberi. I sottoalberi differiscono dall'albero che li contiene per le coordinate del punto di partenza, dell'angolo di rotazione, della lunghezza del tronco e del numero di rami che contengono (uno in meno). Tutte queste differenze dovrebbero essere rese parametri della procedura ricorsiva. Di seguito è presentato un esempio di tale procedura, scritta in Delphi: Procedure Tree(Canvas: TCanvas; //Canvas su cui verrà disegnato l'albero x,y: esteso; //Coordinate della radice Angolo: esteso; //Angolo al quale cresce l'albero TrunkLength: esteso; //Lunghezza del tronco n: intero / /Numero di rami (quante //rimangono chiamate ricorsive)); var x2, y2: esteso; // Fine del tronco (punto di diramazione) inizio x2:= x + TrunkLength * cos(Angle); y2:= y - Lunghezza tronco * sin(Angolo); Canvas.MoveTo(round(x), round(y)); Canvas.LineTo(round(x2), round(y2)); se n > 1 allora inizia Tree(Canvas, x2, y2, Angle+Pi/4, 0.55*TrunkLength, n-1); Albero(Tela, x2, y2, Angolo-Pi/4, 0,55*Lunghezza tronco, n-1); FINE; FINE; Per ottenere la Fig. 6 questa procedura è stata richiamata con i seguenti parametri: Albero(Immagine1.Canvas, 175, 325, Pi/2, 120, 15); Si noti che il disegno viene eseguito prima delle chiamate ricorsive, ovvero l'albero viene disegnato in ordine diretto. Secondo la leggenda nel Grande Tempio di Banaras, sotto la cattedrale che segna il centro del mondo, si trova un disco di bronzo su cui sono fissate 3 aste di diamante, alte un cubito e spesse come un'ape. Molto tempo fa, all'inizio dei tempi, i monaci di questo monastero si offesero davanti al dio Brahma. Infuriato, Brahma eresse tre alte aste e pose 64 dischi d'oro puro su una di esse, in modo che ogni disco più piccolo poggiasse su uno più grande. Non appena tutti i 64 dischi verranno trasferiti dall'asta su cui Dio Brahma li pose durante la creazione del mondo, a un'altra asta, la torre insieme al tempio si trasformeranno in polvere e il mondo perirà sotto i tuoni. Indipendentemente da Brahma, questo enigma fu proposto alla fine del XIX secolo dal matematico francese Edouard Lucas. La versione venduta utilizzava solitamente 7-8 dischi (Fig. 7). Riso. 7. Puzzle “Torri di Hanoi”. Supponiamo che esista una soluzione per N-1 disco. Poi per lo spostamento N dischi, procedere come segue: 1) Spostamento N-1 disco. Perché per il caso N= 1 l'algoritmo di riordinamento è ovvio, quindi per induzione, utilizzando le azioni (1) – (3), possiamo riordinare un numero arbitrario di dischi. Creiamo una procedura ricorsiva che stampi l'intera sequenza di riarrangiamenti per un dato numero di dischi. Ogni volta che viene chiamata tale procedura, deve stampare le informazioni su un turno (dal punto 2 dell'algoritmo). Per i riarrangiamenti dai punti (1) e (3), la procedura si chiamerà da sola con il numero di dischi ridotto di uno. //n – numero di dischi //a, b, c – numeri di pin. Lo spostamento avviene dal pin a, //al pin b con il pin ausiliario c. procedura Hanoi(n, a, b, c: intero); comincia se n > 1 allora inizia Hanoi(n-1, a, c, b); writeln(a, " -> ", b); Hanoi(n-1, c, b, a); end else writeln(a, " -> ", b); FINE; Si noti che l'insieme delle procedure chiamate ricorsivamente in questo caso forma un albero attraversato in ordine inverso. Il compito dell'analisi è calcolare il valore dell'espressione utilizzando una stringa esistente contenente un'espressione aritmetica e i valori noti delle variabili in essa incluse. Il processo di calcolo delle espressioni aritmetiche può essere rappresentato come un albero binario. Ciascuno degli operatori aritmetici (+, –, *, /), infatti, richiede due operandi, che saranno anch'essi espressioni aritmetiche e, di conseguenza, potranno essere considerati come sottoalberi. Riso. La Figura 8 mostra un esempio di albero corrispondente all'espressione: Riso. 8. Albero sintattico corrispondente all'espressione aritmetica (6). In un tale albero, i nodi finali saranno sempre variabili (qui X) o costanti numeriche e tutti i nodi interni conterranno operatori aritmetici. Per eseguire un operatore è necessario prima valutarne gli operandi. Pertanto, l'albero nella figura dovrebbe essere attraversato in ordine terminale. Sequenza corrispondente di nodi chiamato notazione polacca inversa espressione aritmetica. Quando costruisci un albero della sintassi, dovresti prestare attenzione alla seguente funzionalità. Se, ad esempio, c'è un'espressione e leggeremo le operazioni di addizione e sottrazione da sinistra a destra, quindi l'albero sintattico corretto conterrà un meno invece di un più (Fig. 9a). In sostanza, questo albero corrisponde all'espressione. È possibile facilitare la creazione di un albero analizzando l'espressione (8) al contrario, da destra a sinistra. In questo caso il risultato è un albero con Fig. 9b, equivalente all'albero 8a, ma senza necessità di sostituzione della segnaletica. Allo stesso modo, da destra a sinistra, è necessario analizzare le espressioni contenenti operatori di moltiplicazione e divisione. Riso. 9. Alberi sintattici per l'espressione UN – B + C durante la lettura da sinistra a destra (a) e da destra a sinistra (b). Questo approccio non elimina completamente la ricorsione. Tuttavia, consente di limitarsi a una sola chiamata a una procedura ricorsiva, il che può essere sufficiente se lo scopo è massimizzare le prestazioni. L'idea di questo approccio è quella di sostituire le chiamate ricorsive con un semplice ciclo che verrà eseguito tante volte quanti sono i nodi nell'albero formato dalle procedure ricorsive. Ciò che verrà fatto esattamente in ogni passaggio dovrebbe essere determinato dal numero del passaggio. Confrontare il numero del passaggio e le azioni necessarie non è un compito banale e in ogni caso dovrà essere risolto separatamente. Ad esempio, diciamo che vuoi fare K cicli nidificati N passaggi in ciascuno: Per i1:= da 0 a n-1 do per i2:= da 0 a n-1 do per i3:= da 0 a n-1 do … Se Kè sconosciuto in anticipo, è impossibile scriverli esplicitamente, come mostrato sopra. Utilizzando la tecnica illustrata nella Sezione 6.5, è possibile ottenere il numero richiesto di cicli annidati utilizzando una procedura ricorsiva: Procedura NestedCycles(Indici: array di numeri interi; n, k, profondità: intero); var i: intero; iniziare se la profondità Per eliminare la ricorsione e ridurre tutto a un ciclo, nota che se numeri i passaggi nel sistema di numerazione radice N, quindi ogni passaggio ha un numero costituito dai numeri i1, i2, i3, ... o dai valori corrispondenti dell'array Indexes. Cioè, i numeri corrispondono ai valori dei contatori dei cicli. Numero del passo in notazione decimale regolare: Ci saranno un totale di passaggi non k. Esaminando i loro numeri nel sistema numerico decimale e convertendoli ciascuno nel sistema radice N, otteniamo i valori dell'indice: M:= giro(IntPotenza(n, k)); per i:= da 0 a M-1 inizia Number:= i; for p:= da 0 a k-1 iniziano Indici := Numero mod n; Numero:= Numero div n; FINE; FaiQualcosa(Indici); FINE; Notiamo ancora una volta che il metodo non è universale e dovrai inventare qualcosa di diverso per ogni attività. 1. Determinare cosa faranno le seguenti procedure e funzioni ricorsive. (a) Cosa stamperà la seguente procedura quando viene chiamato Rec(4)? Procedura Rec(a: intero); iniziare writeln(a); se a>0 allora Rec(a-1); writeln(a); FINE; (b) Quale sarà il valore della funzione Nod(78, 26)? Funzione Nod(a, b: intero): intero; comincia se a > b allora Nod:= Nod(a – b, b) else if b > a then Nod:= Nod(a, b – a) else Nod:= a; FINE; (c) Cosa verrà stampato con le procedure seguenti quando viene chiamato A(1)? Procedura A(n: intero); procedura B(n: intero); procedura A(n: intero); iniziare writeln(n); B(n-1); FINE; procedura B(n: intero); iniziare writeln(n); se n (d) Cosa verrà stampato dalla procedura seguente quando si chiama BT(0, 1, 3)? Procedura BT(x: reale; D, MaxD: intero); inizia se D = MaxD allora scriviln(x) altrimenti inizia BT(x – 1, D + 1, MaxD); BT(x + 1, D + 1, MaxD); FINE; FINE; 2. Ouroboros - un serpente che divora la propria coda (Fig. 14) quando è aperto ha una lunghezza l, diametro intorno alla testa D, spessore della parete addominale D. Determina quanta coda può infilare dentro di sé e in quanti strati verrà posizionata successivamente? Riso. 14. Ouroboro espanso. 3. Per l'albero in Fig. 10a indicano la sequenza dei nodi di visita in ordine di attraversamento avanti, indietro e finale. 4. Rappresenta graficamente l'albero definito utilizzando parentesi nidificate: (A(B(C, D), E), F, G). 5. Rappresenta graficamente l'albero della sintassi per la seguente espressione aritmetica: Scrivi questa espressione in notazione polacca inversa. 6. Per il grafico sottostante (Fig. 15), annotare la matrice di adiacenza e la matrice di incidenza. 1. Dopo aver calcolato il fattoriale un numero sufficientemente elevato di volte (un milione o più), confrontare l'efficacia degli algoritmi ricorsivi e iterativi. Quanto differirà il tempo di esecuzione e in che modo questo rapporto dipenderà dal numero di cui viene calcolato il fattoriale? 2. Scrivere una funzione ricorsiva che controlli se le parentesi sono posizionate correttamente in una stringa. Se la disposizione è corretta, sono soddisfatte le seguenti condizioni: (a) il numero delle parentesi di apertura e di chiusura è uguale. Esempi di posizionamento errato:)(, ())(, ())((), ecc. 3. La riga può contenere sia parentesi tonde che quadre. Ad ogni parentesi di apertura corrisponde una parentesi di chiusura dello stesso tipo (tonda - tonda, quadra - quadra). Scrivi una funzione ricorsiva che controlli se le parentesi sono posizionate correttamente in questo caso. Esempio di posizionamento errato: ([)]. 4. Il numero di strutture di parentesi regolari di lunghezza 6 è 5: ()()(), (())(), ()(()), ((())), (()()). Nota: Corretta struttura delle parentesi di lunghezza minima "()". Strutture di lunghezza maggiore si ottengono da strutture di lunghezza minore in due modi: (a) se la struttura più piccola è inclusa tra parentesi, 5. Creare una procedura che stampi tutte le possibili permutazioni degli interi da 1 a N. 6. Creare una procedura che stampi tutti i sottoinsiemi dell'insieme (1, 2, ..., N). 7. Creare una procedura che stampi tutte le possibili rappresentazioni del numero naturale N come somma di altri numeri naturali. 8. Creare una funzione che calcoli la somma degli elementi dell'array utilizzando il seguente algoritmo: l'array viene diviso a metà, le somme degli elementi in ciascuna metà vengono calcolate e sommate. La somma degli elementi presenti a metà dell'array viene calcolata utilizzando lo stesso algoritmo, ovvero dividendo nuovamente a metà. Le divisioni avvengono fino a quando i pezzi risultanti dell'array contengono un elemento ciascuno e il calcolo della somma, di conseguenza, diventa banale. Commento: Questo algoritmo è un'alternativa. Nel caso di array con valori reali, in genere consente errori di arrotondamento minori. 10. Creare una procedura che disegna la curva di Koch (Figura 12). 11. Riproduci la figura. 16. Nella figura, ad ogni iterazione successiva il cerchio è 2,5 volte più piccolo (questo coefficiente può essere reso parametro). 1. D.Knuth. L'arte della programmazione informatica. v. 1. (sezione 2.3. “Alberi”).
Ciao N2
…
Ciao N10
…
Ciao N1
…
Ciao N10
Ciao N10
…
Ciao N14. Relazioni di ricorrenza. Ricorsione e iterazione
5. Alberi
5.1. Definizioni di base. Modi per rappresentare gli alberi
a) C'è un nodo speciale chiamato radice di questo albero.
b) I restanti nodi (esclusa la radice) sono contenuti in sottoinsiemi disgiunti a coppie, ciascuno dei quali a sua volta è un albero. Gli alberi vengono chiamati sottoalberi di questo albero.

5.2. Alberi che passano
5.3. Rappresentazione di un albero nella memoria del computer


6. Esempi di algoritmi ricorsivi
6.1. Disegnare un albero

6.2. Torri di Hanoi
Il processo richiede che il disco più grande non finisca mai sopra quello più piccolo. I monaci sono di fronte a un dilemma: in quale ordine dovrebbero fare i turni? È necessario fornire loro il software per calcolare questa sequenza.
2) Spostamento N il disco sul rimanente perno libero.
3) Spostiamo la pila da N-1 disco ricevuto al punto (1) in alto N-esimo disco.6.3. Analisi di espressioni aritmetiche

7.3. Determinare un nodo dell'albero in base al suo numero
Domande di controllo


Compiti
(b) all'interno di ogni coppia c'è una parentesi di apertura - chiusura corrispondente, le parentesi sono posizionate correttamente.
Scrivere un programma ricorsivo per generare tutte le strutture di parentesi regolari di lunghezza 2 N.
(b) se due strutture più piccole vengono scritte in sequenza.
Letteratura
2. N. Wirth. Algoritmi e strutture dati.



