Dadas dos funciones recursivas f y g. Recursividad y algoritmos recursivos. Definiciones basicas. Formas de representar árboles.

Se creó una presentación sobre el tema "Algoritmos recursivos" para preparar a los estudiantes para el Examen Estatal Unificado en informática y TIC. El trabajo examina la definición de recursividad y proporciona ejemplos de objetos gráficos definidos de forma recursiva. La presentación contiene métodos para resolver la tarea número 11 del borrador de la versión de demostración del Examen Estatal Unificado - 2015 en informática. El primer método implica construir un árbol de llamadas, el segundo método resuelve el problema utilizando el método de sustitución. Se consideran 4 ejemplos de resolución de tareas utilizando ambos métodos. La siguiente presentación contiene 25 ejercicios de entrenamiento con respuestas del sitio web de Konstantin Polyakov.

Descargar:

Avance:

Para utilizar vistas previas de presentaciones, cree una cuenta de Google e inicie sesión en ella: https://accounts.google.com

Títulos de diapositivas:

Tarea No. 11 Examen del Estado Unificado (nivel básico, tiempo - 5 minutos) Algoritmos recursivos. Autor – Korotun O.V., profesor de informática, Institución Educativa Municipal “Escuela Secundaria No. 71”

Lo que necesita saber: La recursividad está en la definición, descripción, representación de un objeto o proceso dentro de este objeto o proceso en sí, es decir, una situación en la que un objeto es parte de sí mismo. El escudo de armas de la Federación de Rusia es un objeto gráfico definido de forma recursiva: en la pata derecha del águila bicéfala representada en él, se sujeta un cetro, que está coronado con una copia más pequeña del escudo de armas. Como en este escudo también hay un cetro en la pata derecha del águila, se obtiene una recursión infinita. Escudo de armas recursivo de Rusia.

En programación, la recursividad es llamar a una función desde sí misma, directamente o a través de otras funciones, por ejemplo, la función A llama a la función B y la función B llama a la función A. El número de llamadas anidadas a una función o procedimiento se llama profundidad de recursividad. Ejemplo de recursividad: Si tienes una mancha de grasa en tu vestido, no te preocupes. Las manchas de aceite se quitan con gasolina. Las manchas de gasolina se quitan con una solución alcalina. El álcali se quita con esencia. Frota el rastro de la esencia con aceite. ¡Pues ya sabes cómo quitar las manchas de aceite!

Asignación de ejemplo: Dado un algoritmo recursivo: procedimiento F(n: entero); comenzar a escribir (n); si norte

Asignación de ejemplo: Dado un algoritmo recursivo: procedimiento F(n: entero); comenzar a escribir (n); si n Diapositiva 9

Asignación de ejemplo: Dado un algoritmo recursivo: procedimiento F(n: entero); comenzar a escribir (n); si n Diapositiva 10

Asignación de ejemplo: Dado un algoritmo recursivo: procedimiento F(n: entero); comenzar a escribir (n); si n Diapositiva 11

15 Ejemplo No. 2: Dado un algoritmo recursivo: procedimiento F(n: entero); comenzar a escribir (n); si norte

Ejemplo No. 2: Dado un algoritmo recursivo: procedimiento F(n: entero); comenzar a escribir (n); si n Diapositiva 13

Ejemplo No. 3: Dado un algoritmo recursivo: procedimiento F(n: entero); comenzar a escribir ("*"); si n > 0 entonces comience F(n-2); F(n div 2) fin fin; ¿Cuántos asteriscos se imprimirán en la pantalla al llamar a F(7)? 7 5 3 2 3 1 1 1 1 En este ejemplo, el símbolo * -2 div 2 1 0 -1 0 -1 0 -1 -1 -1 0 0 0 se muestra en la pantalla en lugar de los valores del parámetro n.

Ejemplo No. 3: Dado un algoritmo recursivo: procedimiento F(n: entero); comenzar a escribir ("*"); si n > 0 entonces comience F(n-2); F(n div 2) fin fin; ¿Cuántos asteriscos se imprimirán en la pantalla al llamar a F(7)? * Al contar el número de “estrellas”, obtenemos 21. En este ejemplo, no son los valores del parámetro n los que se muestran en la pantalla, sino el símbolo * * * * * * * * * * * * * * * * * * * * * *

Ejemplo No. 3: Dado un algoritmo recursivo: procedimiento F(n: entero); comenzar a escribir ("*"); si n > 0 entonces comience F(n-2); F(n div 2) fin fin; ¿Cuántos asteriscos se imprimirán en la pantalla al llamar a F(7)? Resolvamos el problema sin árbol. Sea S(n) el número de “estrellas” que se imprimirán al llamar a F(n). Entonces 1+S(n-2)+ S(n div 2), n>0 1 , n Necesitamos saber S(7). S(7)= 1 +S(5)+ S(3) S(5)= 1 +S(3)+S(2) S(3)= 1 +S(1)+S(1) S( 2)=1+S(0)+S(1)=1+1+S(1)=2+S(1) S(1)= 1+ S(-1)+S(0)=1+ 1+1=3 Inversa: S(2)=2+3=5 S(3)=1+3+3=7 S(5)=1+7+5=13 S(7)=1+ 13+ 7= 21S(n)=

Ejemplo No. 4: procedimiento F(n: entero); comenzar si n Diapositiva 18

Ejemplo No. 4: procedimiento F(n: entero); comenzar si n Diapositiva 19

Ejemplo No. 4: procedimiento F(n: entero); comenzar si n

Tareas de entrenamiento

Problema 1: Dado un algoritmo recursivo: procedimiento F(n: entero); comenzar a escribir ("*"); si n > 0 entonces comience F(n-2); F(n div 2); F(n div 2); fin fin ; ¿Cuántos asteriscos se imprimirán en la pantalla al llamar a F(5)? Respuesta: 34

Problema 2: Dado un algoritmo recursivo: procedimiento F(n: entero); comenzar a escribir ("*"); si n > 0 entonces comience F(n-2); F(n-2); F(n div 2); fin fin ; ¿Cuántos asteriscos se imprimirán en la pantalla al llamar a F(6)? Respuesta: 58

Problema 3: Dado un algoritmo recursivo: procedimiento F(n: entero); comenzar a escribir ("*"); si n > 0 entonces comience F(n-3); F(n div 2); fin fin ; ¿Cuántos asteriscos se imprimirán en la pantalla al llamar a F(7)? Respuesta: 15

Problema 4: Dado un algoritmo recursivo: procedimiento F(n: entero); comenzar a escribir ("*"); si n > 0 entonces comience F(n-3); F(n-2); F(n div 2); fin fin ; ¿Cuántos asteriscos se imprimirán en la pantalla al llamar a F(7)? Respuesta: 55

Problema 5: Dado un algoritmo recursivo: procedimiento F(n: entero); comenzar a escribir ("*"); si n > 0 entonces comience F(n-3); F(n-2); F(n div 2); F(n div 2); fin fin ; ¿Cuántos asteriscos se imprimirán en la pantalla al llamar a F(6)? Respuesta: 97

Problema 6: Dado un algoritmo recursivo: procedimiento F(n: entero); comenzar a escribir ("*"); si n > 0 entonces comience writeln("*"); F(n-2); F(n div 2); fin fin ; ¿Cuántos asteriscos se imprimirán en la pantalla al llamar a F(7)? Respuesta: 31

Problema 7: Dado un algoritmo recursivo: procedimiento F(n: entero); comenzar a escribir ("*"); si n > 0 entonces comience writeln("*"); F(n-2); F(n div 2); F(n div 2); fin fin; ¿Cuántos asteriscos se imprimirán en la pantalla al llamar a F(7)? Respuesta: 81

Problema 8: Dado un algoritmo recursivo: procedimiento F(n: entero); comenzar a escribir ("*"); si n > 0 entonces comience writeln("*"); F(n-2); F(n-2); F(n div 2); fin fin; ¿Cuántos asteriscos se imprimirán en la pantalla al llamar a F(6)? Respuesta: 77

Problema 9: Dado un algoritmo recursivo: procedimiento F(n: entero); comience si n > 0 entonces comience F(n-2); F(n-1); F(n-1); fin; escrito("*"); fin ; ¿Cuántos asteriscos se imprimirán en la pantalla al llamar a F(5)? Respuesta: 148

Problema 10: Dado un algoritmo recursivo: procedimiento F(n: entero); comenzar si n > 0 entonces comenzar writeln("*"); F(n-2); F(n-1); F(n-1); fin; escrito("*"); fin; ¿Cuántos asteriscos se imprimirán en la pantalla al llamar a F(5)? Respuesta: 197

Problema 11: Dado un algoritmo recursivo: procedimiento F(n: entero); comenzar si n > 1 entonces comenzar F(n-2); F(n-1); F(n div 2); fin; escrito("*"); fin ; ¿Cuántos asteriscos se imprimirán en la pantalla al llamar a F(7)? Respuesta: 88

Problema 12: Dado un algoritmo recursivo: procedimiento F(n: entero); comience si n > 2 entonces comience writeln("*"); F(n-2); F(n-1); F(n div 2); fin ; escrito("*"); fin; ¿Cuántos asteriscos se imprimirán en la pantalla al llamar a F(6)? Respuesta: 33

Problema 13: Dado un algoritmo recursivo: procedimiento F (n: entero); comenzar a escribir (n); si norte

Problema 14: Dado un algoritmo recursivo: procedimiento F (n: entero); comenzar a escribir (n); si norte

Problema 15: Dado un algoritmo recursivo: procedimiento F (n: entero); comenzar a escribir (n); si norte

Problema 16: Dado un algoritmo recursivo: procedimiento F (n: entero); comenzar a escribir (n); si norte

Problema 17: Dado un algoritmo recursivo: procedimiento F (n: entero); comenzar a escribir (n); si norte

Problema 18: Dado un algoritmo recursivo: procedimiento F (n: entero); comenzar a escribir (n); si norte

Problema 19: Dado un algoritmo recursivo: procedimiento F (n: entero); comenzar a escribir (n); si norte

Problema 20: Dado un algoritmo recursivo: procedimiento F (n: entero); comenzar a escribir (n); si norte

Problema 21: Dado un algoritmo recursivo: procedimiento F (n: entero); comenzar a escribir (n); si norte

Problema 22: Dado un algoritmo recursivo: procedimiento F (n: entero); comenzar a escribir (n); si norte

Problema 23: Dado un algoritmo recursivo: procedimiento F (n: entero); comenzar a escribir (n); si norte

Problema 24: Dado un algoritmo recursivo: procedimiento F (n: entero); comenzar a escribir (n); si norte

Problema 25: Dado un algoritmo recursivo: procedimiento F (n: entero); comenzar a escribir (n); si norte

La recursividad es cuando una subrutina se llama a sí misma. Al enfrentarse por primera vez a un diseño algorítmico de este tipo, la mayoría de las personas experimentan ciertas dificultades, pero con un poco de práctica, la recursividad se convertirá en una herramienta comprensible y muy útil en su arsenal de programación.

1. La esencia de la recursividad

Un procedimiento o función puede contener llamadas a otros procedimientos o funciones. El procedimiento también puede llamarse a sí mismo. No hay ninguna paradoja aquí: la computadora solo ejecuta secuencialmente los comandos que encuentra en el programa y, si encuentra una llamada a un procedimiento, simplemente comienza a ejecutar este procedimiento. No importa qué procedimiento dio la orden para hacer esto.

Ejemplo de un procedimiento recursivo:

Procedimiento Rec(a: entero); comenzar si a>

Consideremos qué sucede si se realiza una llamada, por ejemplo, de la forma Rec(3) en el programa principal. A continuación se muestra un diagrama de flujo que muestra la secuencia de ejecución de las declaraciones.

Arroz. 1. Diagrama de bloques del procedimiento recursivo.

El procedimiento Rec se llama con el parámetro a = 3. Contiene una llamada al procedimiento Rec con el parámetro a = 2. La llamada anterior aún no se ha completado, por lo que puedes imaginar que se crea otro procedimiento y el primero no termina su trabajo hasta termina. El proceso de llamada finaliza cuando el parámetro a = 0. En este punto, se ejecutan 4 instancias del procedimiento simultáneamente. El número de procedimientos realizados simultáneamente se llama profundidad de recursividad.

El cuarto procedimiento llamado (Rec(0)) imprimirá el número 0 y finalizará su trabajo. Después de esto, el control regresa al procedimiento que lo llamó (Rec(1)) y se imprime el número 1. Y así sucesivamente hasta completar todos los procedimientos. La llamada original imprimirá cuatro números: 0, 1, 2, 3.

Otra imagen visual de lo que está sucediendo se muestra en la Fig. 2.

Arroz. 2. Ejecutar el procedimiento Rec con el parámetro 3 consiste en ejecutar el procedimiento Rec con el parámetro 2 e imprimir el número 3. A su vez ejecutar el procedimiento Rec con el parámetro 2 consiste en ejecutar el procedimiento Rec con el parámetro 1 e imprimir el número 2. Etc .

Como ejercicio por su cuenta, considere lo que sucede cuando llama a Rec(4). Considere también lo que sucedería si llamara al procedimiento Rec2(4) siguiente, con los operadores invertidos.

Procedimiento Rec2(a: entero); comenzar a escribir (a); si a>0 entonces Rec2(a-1); fin;

Tenga en cuenta que en estos ejemplos la llamada recursiva está dentro de una declaración condicional. Esta es una condición necesaria para que la recursividad termine alguna vez. También tenga en cuenta que el procedimiento se llama a sí mismo con un parámetro diferente al que fue llamado. Si el procedimiento no utiliza variables globales, esto también es necesario para que la recursividad no continúe indefinidamente.

Es posible un esquema un poco más complejo: la función A llama a la función B, que a su vez llama a A. Esto se llama recursividad compleja. Resulta que el procedimiento descrito primero debe llamar a un procedimiento que aún no ha sido descrito. Para que esto sea posible, es necesario utilizar .

Procedimiento A(n: número entero); (Descripción directa (encabezado) del primer procedimiento) procedimiento B(n: entero); (Descripción directa del segundo procedimiento) procedimiento A(n: entero); (Descripción completa del procedimiento A) start writeln(n); B(n-1); fin; procedimiento B(n: número entero); (Descripción completa del procedimiento B) start writeln(n); si norte

La declaración directa del procedimiento B permite que se llame desde el procedimiento A. La declaración directa del procedimiento A no es necesaria en este ejemplo y se agrega por razones estéticas.

Si la recursividad ordinaria se puede comparar con un ouroboros (Fig. 3), entonces la imagen de la recursividad compleja se puede extraer del famoso poema infantil, donde "Los lobos se asustaron y se comieron unos a otros". Imagine dos lobos comiéndose entre sí y comprenderá la recursividad compleja.

Arroz. 3. Ouroboros: una serpiente que se devora su propia cola. Dibujo del tratado de alquimia "Synosius" de Theodore Pelecanos (1478).

Arroz. 4. Recursión compleja.

3. Simular un bucle mediante recursividad

Si un procedimiento se llama a sí mismo, esencialmente hace que las instrucciones que contiene se ejecuten nuevamente, de manera similar a un bucle. Algunos lenguajes de programación no contienen ninguna construcción de bucle, lo que permite a los programadores organizar las repeticiones mediante la recursividad (por ejemplo, Prolog, donde la recursividad es una técnica de programación básica).

Por ejemplo, simulemos el funcionamiento de un bucle for. Para ello necesitamos una variable de contador de pasos, que se puede implementar, por ejemplo, como parámetro de procedimiento.

Ejemplo 1.

Procedimiento LoopImitation(i, n: entero); (El primer parámetro es el contador de pasos, el segundo parámetro es el número total de pasos) start writeln("Hola N ", i); //Aquí hay instrucciones que se repetirán si

El resultado de una llamada del formulario LoopImitation(1, 10) será la ejecución de instrucciones diez veces, cambiando el contador de 1 a 10. En este caso se imprimirá lo siguiente:

Hola n 1
Hola n2
…
Hola n 10

En general, no es difícil ver que los parámetros del procedimiento son los límites para cambiar los valores del contador.

Puede intercambiar la llamada recursiva y las instrucciones que se repetirán, como en el siguiente ejemplo.

Ejemplo 2.

Procedimiento LoopImitation2(i, n: entero); empezar si yo

En este caso, se producirá una llamada a un procedimiento recursivo antes de que comiencen a ejecutarse las instrucciones. La nueva instancia del procedimiento también llamará, en primer lugar, a otra instancia, y así sucesivamente, hasta alcanzar el valor máximo del contador. Sólo después de esto el último de los procedimientos llamados ejecutará sus instrucciones, luego el penúltimo ejecutará sus instrucciones, etc. El resultado de llamar a LoopImitation2(1, 10) será imprimir saludos en orden inverso:

Hola n 10
…
Hola n 1

Si imaginamos una cadena de procedimientos llamados recursivamente, entonces en el ejemplo 1 la recorremos desde los procedimientos llamados anteriormente hasta los posteriores. En el ejemplo 2, por el contrario, de más tarde a más temprano.

Finalmente, se puede realizar una llamada recursiva entre dos bloques de instrucciones. Por ejemplo:

Procedimiento LoopImitation3(i, n: entero); comenzar a escribir ("Hola N", i); (El primer bloque de instrucciones puede estar ubicado aquí) si

Aquí, las instrucciones del primer bloque se ejecutan primero de forma secuencial y luego las instrucciones del segundo bloque se ejecutan en orden inverso. Al llamar a LoopImitation3(1, 10) obtenemos:

Hola n 1
…
Hola n 10
Hola n 10
…
Hola n 1

Se necesitarían dos bucles para hacer lo mismo sin recursividad.

Puedes aprovechar que la ejecución de partes de un mismo procedimiento se espacia en el tiempo. Por ejemplo:

Ejemplo 3: convertir un número a binario.

La obtención de los dígitos de un número binario, como saben, se produce dividiendo con resto por la base del sistema numérico 2. Si hay un número, entonces su último dígito en su representación binaria es igual a

Tomando toda la parte de la división por 2:

obtenemos un número que tiene la misma representación binaria, pero sin el último dígito. Por lo tanto, basta con repetir las dos operaciones anteriores hasta que el siguiente campo de división reciba una parte entera igual a 0. Sin recursividad se verá así:

Mientras que x>0 comienza c:=x mod 2; x:=x div 2; escribir(c); fin;

El problema aquí es que los dígitos de la representación binaria se calculan en orden inverso (el último primero). Para imprimir un número en forma normal, deberá recordar todos los números en los elementos de la matriz e imprimirlos en un bucle separado.

Usando la recursividad, no es difícil lograr resultados en el orden correcto sin una matriz y un segundo bucle. A saber:

Procedimiento BinaryRepresentation(x: entero); var c, x: entero; comenzar (Primer bloque. Ejecutado en orden de llamadas a procedimientos) c:= x mod 2; x:= x div 2; (Llamada recursiva) si x>0 entonces BinaryRepresentation(x); (Segundo bloque. Ejecutado en orden inverso) write(c); fin;

En términos generales, no recibimos ninguna ganancia. Los dígitos de la representación binaria se almacenan en variables locales, que son diferentes para cada instancia en ejecución del procedimiento recursivo. Es decir, no fue posible ahorrar memoria. Por el contrario, desperdiciamos memoria extra almacenando muchas variables locales x. Sin embargo, esta solución me parece hermosa.

4. Relaciones de recurrencia. Recursión e iteración

Se dice que una secuencia de vectores está dada por una relación de recurrencia si se dan el vector inicial y la dependencia funcional del vector posterior respecto del anterior.

Un ejemplo simple de una cantidad calculada usando relaciones de recurrencia es el factorial.

El siguiente factorial se puede calcular a partir del anterior como:

Introduciendo la notación , obtenemos la relación:

Los vectores de la fórmula (1) se pueden interpretar como conjuntos de valores variables. Luego, el cálculo del elemento requerido de la secuencia consistirá en la actualización repetida de sus valores. En particular para factorial:

X:= 1; para i:= 2 an hacer x:= x * i; escribir(x);

Cada una de estas actualizaciones (x:= x * i) se llama iteración, y el proceso de repetir iteraciones es iteración.

Notemos, sin embargo, que la relación (1) es una definición puramente recursiva de la secuencia y el cálculo del enésimo elemento es en realidad la toma repetida de la función f de sí misma:

En particular, para factorial se puede escribir:

Función Factorial(n: entero): entero; comenzar si n > 1 entonces Factorial:= n * Factorial(n-1) else Factorial:= 1; fin;

Debe entenderse que llamar a funciones implica una sobrecarga adicional, por lo que la primera opción para calcular el factorial será un poco más rápida. En general, las soluciones iterativas funcionan más rápido que las recursivas.

Antes de pasar a situaciones en las que la recursividad es útil, veamos un ejemplo más en el que no debería utilizarse.

Consideremos un caso especial de relaciones recurrentes, cuando el siguiente valor de la secuencia no depende de uno, sino de varios valores anteriores a la vez. Un ejemplo es la famosa secuencia de Fibonacci, en la que cada elemento siguiente es la suma de los dos anteriores:

Con un enfoque “frontal”, puedes escribir:

Función Fib(n: entero): entero; comience si n > 1 entonces Fib:= Fib(n-1) + Fib(n-2) de lo contrario Fib:= 1; fin;

Cada llamada de Fib crea dos copias de sí misma, cada copia crea dos más, y así sucesivamente. El número de operaciones aumenta con el número norte exponencialmente, aunque con una solución iterativa lineal en norte número de operaciones.

De hecho, el ejemplo anterior nos enseña que no CUANDO La recursividad no debe usarse, de lo contrario CÓMO No debería ser usado. Después de todo, si existe una solución iterativa rápida (basada en bucles), entonces el mismo bucle se puede implementar mediante un procedimiento o función recursiva. Por ejemplo:

// x1, x2 – condiciones iniciales (1, 1) // n – número de la función de número de Fibonacci requerida Fib(x1, x2, n: entero): entero; var x3: entero; comenzar si n > 1 entonces comenzar x3:= x2 + x1; x1:= x2; x2:= x3; Fib:= Fib(x1, x2, n-1); fin más Fib:= x2; fin;

Aún así, son preferibles las soluciones iterativas. La pregunta es, ¿cuándo se debe utilizar la recursividad en este caso?

Cualquier procedimiento y función recursiva que contenga solo una llamada recursiva a sí mismo puede reemplazarse fácilmente por bucles iterativos. Para obtener algo que no tenga una contraparte simple no recursiva, es necesario recurrir a procedimientos y funciones que se autodenominan dos o más veces. En este caso, el conjunto de procedimientos llamados ya no forma una cadena, como en la Fig. 1, sino un árbol entero. Existen amplias clases de problemas en los que el proceso computacional debe organizarse de esta manera. Para ellos, la recursividad será la solución más sencilla y natural.

5. árboles

La base teórica de las funciones recursivas que se llaman a sí mismas más de una vez es la rama de las matemáticas discretas que estudia los árboles.

5.1. Definiciones basicas. Formas de representar árboles.

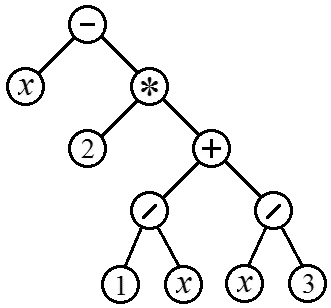
Definición: llamaremos al conjunto finito t, que consta de uno o más nodos tales que:
a) Hay un nodo especial llamado raíz de este árbol.
b) Los nodos restantes (excluyendo la raíz) están contenidos en subconjuntos disjuntos por pares, cada uno de los cuales a su vez es un árbol. Los árboles se llaman subárboles de este árbol.

Esta definición es recursiva. En resumen, un árbol es un conjunto formado por una raíz y subárboles adjuntos a ella, que también son árboles. Un árbol se define a través de sí mismo. Sin embargo, esta definición tiene sentido porque la recursividad es finita. Cada subárbol contiene menos nodos que el árbol que lo contiene. Al final, llegamos a subárboles que contienen solo un nodo, y ya está claro de qué se trata.

Arroz. 3. Árbol.

En la Fig. La Figura 3 muestra un árbol con siete nodos. Aunque los árboles comunes crecen de abajo hacia arriba, es costumbre dibujarlos al revés. Al dibujar un diagrama a mano, este método es obviamente más conveniente. Debido a esta inconsistencia, a veces surge confusión cuando se dice que un nodo está encima o debajo de otro. Por esta razón, es más conveniente utilizar la terminología utilizada al describir árboles genealógicos, llamando a los nodos más cercanos a la raíz ancestros y a los más distantes, descendientes.

Un árbol se puede representar gráficamente de otras formas. Algunos de ellos se muestran en la Fig. 4. Según la definición, un árbol es un sistema de conjuntos anidados, donde estos conjuntos no se cruzan o están completamente contenidos uno en otro. Estos conjuntos se pueden representar como regiones en un plano (Fig. 4a). En la Fig. 4b, los conjuntos anidados no están situados en un plano, sino que están alargados formando una línea. Arroz. 4b también puede verse como un diagrama de alguna fórmula algebraica que contiene paréntesis anidados. Arroz. La Figura 4c ofrece otra forma popular de representar una estructura de árbol como una lista escalonada.

Arroz. 4. Otras formas de representar estructuras de árboles: (a) conjuntos anidados; (b) paréntesis anidados; (c) lista de concesiones.

La lista escalonada tiene similitudes obvias con la forma en que se formatea el código del programa. De hecho, un programa escrito dentro del marco del paradigma de programación estructurada se puede representar como un árbol que consta de estructuras anidadas.

También se puede establecer una analogía entre la lista escalonada y la apariencia de las tablas de contenido de los libros, donde las secciones contienen subsecciones, que a su vez contienen subsecciones, etc. La forma tradicional de numerar dichas secciones (sección 1, subsecciones 1.1 y 1.2, subsección 1.1.2, etc.) se denomina sistema decimal de Dewey. Aplicado al árbol de la Fig. 3 y 4 este sistema dará:

1.A; 1,1 mil millones; 1,2ºC; 1.2.1 D; 1.2.2 E; 1.2.3F; 1.2.3.1 G;

5.2. Pasando árboles

En todos los algoritmos relacionados con estructuras de árbol, aparece invariablemente la misma idea, es decir, la idea paso o recorrido del árbol. Esta es una forma de visitar los nodos del árbol en la que cada nodo se recorre exactamente una vez. Esto da como resultado una disposición lineal de los nodos del árbol. En particular, hay tres formas: puede recorrer los nodos en orden directo, inverso y final.

Algoritmo de recorrido hacia adelante:

Llegar a la raíz
Recorra todos los subárboles de izquierda a derecha en orden directo.

Este algoritmo es recursivo, ya que el recorrido de un árbol contiene el recorrido de subárboles, y estos, a su vez, se recorren utilizando el mismo algoritmo.

En particular, para el árbol de la Fig. 3 y 4, el recorrido directo da una secuencia de nodos: A, B, C, D, E, F, G.

La secuencia resultante corresponde a una enumeración de nodos de izquierda a derecha cuando se representa un árbol usando paréntesis anidados y en notación decimal Dewey, así como un pasaje de arriba hacia abajo cuando se representa como una lista escalonada.

Al implementar este algoritmo en un lenguaje de programación, llegar a la raíz corresponde a que el procedimiento o función realiza algunas acciones, y atravesar subárboles corresponde a llamadas recursivas a sí mismo. En particular, para un árbol binario (donde cada nodo tiene como máximo dos subárboles), el procedimiento correspondiente sería el siguiente:

// Preorder Traversal – nombre en inglés para el procedimiento de pedido directo PreorderTraversal((Arguments)); comenzar //Pasando la raíz DoSomething((Arguments)); //Transición del subárbol izquierdo si (Hay un subárbol izquierdo) entonces PreorderTransversal((Argumentos 2)); //Transición del subárbol derecho si (Hay un subárbol derecho) entonces PreorderTransversal((Argumentos 3)); fin;

Es decir, primero el procedimiento realiza todas las acciones y sólo entonces se producen todas las llamadas recursivas.

Algoritmo de recorrido inverso:

Pasa por el subárbol izquierdo,
Llegar a la raíz
Pase por el siguiente subárbol a la izquierda.
Llegar a la raíz
etc. hasta que se atraviese el subárbol más a la derecha.

Es decir, todos los subárboles se atraviesan de izquierda a derecha y el retorno a la raíz se encuentra entre estos recorridos. Para el árbol de la Fig. 3 y 4 esto da la secuencia de nodos: B, A, D, C, E, G, F.

En un procedimiento recursivo correspondiente, las acciones se ubicarán en los espacios entre las llamadas recursivas. Específicamente para un árbol binario:

// Inorder Traversal – nombre en inglés para el procedimiento de orden inverso InorderTraversal((Arguments)); comenzar // Viajando por el subárbol izquierdo si (Existe un subárbol izquierdo) entonces InorderTraversal((Argumentos 2)); //Pasando la raíz DoSomething((Arguments)); //Atraviesa el subárbol derecho si (existe un subárbol derecho) entonces InorderTraversal((Argumentos 3)); fin;

Algoritmo transversal de orden final:

Recorra todos los subárboles de izquierda a derecha,
Llega a la raíz.

Para el árbol de la Fig. 3 y 4 esto dará la secuencia de nodos: B, D, E, G, F, C, A.

En un procedimiento recursivo correspondiente, las acciones se ubicarán después de las llamadas recursivas. Específicamente para un árbol binario:

// Postorder Traversal – nombre en inglés para el procedimiento de orden final PostorderTraversal((Arguments)); comenzar // Viajando por el subárbol izquierdo si (hay un subárbol izquierdo) entonces PostorderTraversal((Argumentos 2)); //Trascendiendo el subárbol derecho si (Existe un subárbol derecho) entonces PostorderTraversal((Argumentos 3)); //Pasando la raíz DoSomething((Arguments)); fin;

5.3. Representación de un árbol en la memoria de la computadora.

Si alguna información se encuentra en los nodos del árbol, entonces se puede utilizar una estructura de datos dinámica adecuada para almacenarla. En Pascal, esto se hace usando una variable de tipo registro que contiene punteros a subárboles del mismo tipo. Por ejemplo, un árbol binario donde cada nodo contiene un número entero se puede almacenar usando una variable de tipo PTree, que se describe a continuación:

Escriba PTree = ^TTree; Ttree = registro Inf: entero; Subárbol izquierdo, Subárbol derecho: PTree; fin;

Cada nodo tiene un tipo PTree. Este es un puntero, lo que significa que cada nodo debe crearse llamando al procedimiento Nuevo en él. Si el nodo es un nodo hoja, entonces a sus campos LeftSubTree y RightSubTree se les asigna el valor nulo. De lo contrario, el procedimiento Nuevo también crea los nodos LeftSubTree y RightSubTree.

Uno de esos registros se muestra esquemáticamente en la Fig. 5.

Arroz. 5. Representación esquemática de un registro tipo Ttree. El registro tiene tres campos: Inf – un número, LeftSubTree y RightSubTree – punteros a registros del mismo tipo TTree.

En la Figura 6 se muestra un ejemplo de un árbol formado por dichos registros.

Arroz. 6. Un árbol formado por registros de tipo Ttree. Cada entrada almacena un número y dos punteros que pueden contener nulo, o direcciones de otros registros del mismo tipo.

Si no ha trabajado anteriormente con estructuras que consisten en registros que contienen enlaces a registros del mismo tipo, le recomendamos que se familiarice con el material al respecto.

6. Ejemplos de algoritmos recursivos

6.1. dibujando un arbol

Consideremos el algoritmo para dibujar el árbol que se muestra en la Fig. 6. Si cada línea se considera un nodo, entonces esta imagen satisface completamente la definición de árbol dada en la sección anterior.

Arroz. 6. Árbol.

El procedimiento recursivo obviamente dibujaría una línea (el tronco hasta la primera rama) y luego se llamaría a sí mismo para dibujar los dos subárboles. Los subárboles se diferencian del árbol que los contiene en las coordenadas de su punto inicial, el ángulo de rotación, la longitud del tronco y el número de ramas que contienen (una menos). Todas estas diferencias deben considerarse parámetros del procedimiento recursivo.

A continuación se presenta un ejemplo de dicho procedimiento, escrito en Delphi:

Procedimiento Árbol(Canvas: TCanvas; //Lienzo sobre el que se dibujará el árbol x,y: extendido; //Coordenadas raíz Ángulo: extendido; //Ángulo en el que crece el árbol TrunkLength: extendido; //Longitud del tronco n: entero //Número de ramas (cuántas //llamadas recursivas más quedan)); var x2, y2: extendido; //Empieza el extremo del tronco (punto de bifurcación) x2:= x + TrunkLength * cos(Angle); y2:= y - Longitud del tronco * sin(Ángulo); Canvas.MoveTo(ronda(x), ronda(y)); Canvas.LineTo(redondo(x2), redondeado(y2)); si n > 1 entonces comience Tree(Canvas, x2, y2, Angle+Pi/4, 0.55*TrunkLength, n-1); Árbol (Lienzo, x2, y2, Ángulo-Pi/4, 0,55*Longitud del tronco, n-1); fin; fin;

Para obtener la Fig. 6 este procedimiento fue llamado con los siguientes parámetros:

Árbol(Imagen1.Canvas, 175, 325, Pi/2, 120, 15);

Tenga en cuenta que el dibujo se realiza antes de las llamadas recursivas, es decir, el árbol se dibuja en orden directo.

6.2. Torres de Hanói

Según la leyenda, en el Gran Templo de Banaras, debajo de la catedral, que marca la mitad del mundo, hay un disco de bronce en el que se fijan 3 varillas de diamantes, de un codo de alto y gruesas como una abeja. Hace mucho tiempo, en el principio de los tiempos, los monjes de este monasterio cometieron ofensas ante el dios Brahma. Enfurecido, Brahma erigió tres varas altas y colocó 64 discos de oro puro en una de ellas, de modo que cada disco más pequeño descansara sobre uno más grande. Tan pronto como los 64 discos sean transferidos de la barra en la que Dios Brahma los colocó al crear el mundo, a otra barra, la torre junto con el templo se convertirán en polvo y el mundo perecerá bajo los truenos.
El proceso requiere que el disco más grande nunca termine encima del más pequeño. Los monjes se encuentran ante un dilema: ¿en qué orden deben hacer los turnos? Es necesario proporcionarles un software para calcular esta secuencia.

Independientemente de Brahma, este rompecabezas fue propuesto a finales del siglo XIX por el matemático francés Edouard Lucas. La versión vendida solía utilizar entre 7 y 8 discos (Fig. 7).

Arroz. 7. Puzzle “Torres de Hanoi”.

Supongamos que existe una solución para norte-1 disco. Entonces para cambiar norte discos, proceda de la siguiente manera:

1) turno norte-1 disco.
2) turno norteº disco en el pasador libre restante.
3) Cambiamos la pila de norte-1 disco recibido en el punto (1) en la parte superior norte-ésimo disco.

porque para el caso norte= 1 el algoritmo de reordenamiento es obvio, entonces por inducción, usando las acciones (1) – (3), podemos reordenar un número arbitrario de discos.

Creemos un procedimiento recursivo que imprima la secuencia completa de reordenamientos para una cantidad determinada de discos. Cada vez que se llama a un procedimiento de este tipo, debe imprimir información sobre un turno (desde el punto 2 del algoritmo). Para reordenamientos de los puntos (1) y (3), el procedimiento se llamará a sí mismo con el número de discos reducido en uno.

//n – número de discos //a, b, c – números de pin. El cambio se realiza desde el pin a, //al pin b con el pin auxiliar c. procedimiento Hanoi(n, a, b, c: entero); comenzar si n > 1 entonces comenzar Hanoi(n-1, a, c, b); writeln(a, " -> ", b); Hanói(n-1, c, b, a); fin más writeln(a, " -> ", b); fin;

Tenga en cuenta que el conjunto de procedimientos llamados recursivamente en este caso forma un árbol atravesado en orden inverso.

6.3. Analizar expresiones aritméticas

La tarea del análisis es calcular el valor de la expresión utilizando una cadena existente que contiene una expresión aritmética y los valores conocidos de las variables incluidas en ella.

El proceso de calcular expresiones aritméticas se puede representar como un árbol binario. De hecho, cada uno de los operadores aritméticos (+, –, *, /) requiere dos operandos, que también serán expresiones aritméticas y, en consecuencia, pueden considerarse subárboles. Arroz. La Figura 8 muestra un ejemplo de árbol correspondiente a la expresión:

Arroz. 8. Árbol sintáctico correspondiente a la expresión aritmética (6).

En dicho árbol, los nodos finales siempre serán variables (aquí X) o constantes numéricas, y todos los nodos internos contendrán operadores aritméticos. Para ejecutar un operador, primero debe evaluar sus operandos. Por tanto, el árbol de la figura debe recorrerse en orden terminal. Secuencia correspondiente de nodos.

llamado notación polaca inversa expresión aritmética.

Al construir un árbol de sintaxis, se debe prestar atención a la siguiente característica. Si, por ejemplo, hay una expresión

y leeremos las operaciones de suma y resta de izquierda a derecha, entonces el árbol de sintaxis correcto contendrá un menos en lugar de un más (Fig. 9a). En esencia, este árbol corresponde a la expresión. Es posible facilitar la creación de un árbol si se analiza la expresión (8) al revés, de derecha a izquierda. En este caso, el resultado es un árbol con la Fig. 9b, equivalente al árbol 8a, pero no requiere reemplazo de señales.

De manera similar, de derecha a izquierda, es necesario analizar expresiones que contengan operadores de multiplicación y división.

Arroz. 9. Árboles de sintaxis para expresión. a – b + C al leer de izquierda a derecha (a) y de derecha a izquierda (b).

Este enfoque no elimina por completo la recursividad. Sin embargo, le permite limitarse a una sola llamada a un procedimiento recursivo, lo que puede ser suficiente si el motivo es maximizar el rendimiento.

7.3. Determinar un nodo de árbol por su número

La idea de este enfoque es reemplazar las llamadas recursivas con un bucle simple que se ejecutará tantas veces como nodos haya en el árbol formado por los procedimientos recursivos. Lo que se hará exactamente en cada paso debe estar determinado por el número de paso. Comparar el número de pasos y las acciones necesarias no es una tarea fácil y en cada caso habrá que resolverlo por separado.

Por ejemplo, digamos que quieres hacer k bucles anidados norte pasos en cada uno:

Para i1:= 0 a n-1 hacer para i2:= 0 a n-1 hacer para i3:= 0 a n-1 hacer…

Si k Se desconoce de antemano, es imposible escribirlos explícitamente, como se muestra arriba. Utilizando la técnica demostrada en la Sección 6.5, puede obtener el número requerido de bucles anidados mediante un procedimiento recursivo:

Procedimiento NestedCycles(Índices: matriz de enteros; n, k, profundidad: entero); var i: entero; comenzar si profundidad

Para deshacerse de la recursividad y reducir todo a un ciclo, tenga en cuenta que si numera los pasos en el sistema numérico de base norte, entonces cada paso tiene un número que consta de los números i1, i2, i3, ... o los valores correspondientes de la matriz Índices. Es decir, los números corresponden a los valores de los contadores de ciclos. Número de paso en notación decimal regular:

Habrá un total de pasos. nk. Revisando sus números en el sistema numérico decimal y convirtiendo cada uno de ellos al sistema de base. norte, obtenemos los valores del índice:

M:= ronda(IntPower(n, k)); para i:= 0 a M-1 comience Número:= i; para p:= 0 a k-1 comience Índices:= Número mod n; Número:= Número div n; fin; Hacer algo (índices); fin;

Notemos una vez más que el método no es universal y tendrás que idear algo diferente para cada tarea.

Preguntas de control

1. Determine qué harán los siguientes procedimientos y funciones recursivos.

(a) ¿Qué imprimirá el siguiente procedimiento cuando se llame a Rec(4)?

Procedimiento Rec(a: entero); comenzar a escribir (a); si a>0 entonces Rec(a-1); escrito(a); fin;

(b) ¿Cuál será el valor de la función Nod(78, 26)?

Función Nod(a, b: entero): entero; comenzar si a > b entonces Nod:= Nod(a – b, b) si no, si b > a entonces Nod:= Nod(a, b – a) más Nod:= a; fin;

Procedimiento A(n: número entero); procedimiento B(n: número entero); procedimiento A(n: número entero); comenzar a escribir (n); B(n-1); fin; procedimiento B(n: número entero); comenzar a escribir (n); si norte

(d) ¿Qué imprimirá el siguiente procedimiento al llamar a BT(0, 1, 3)?

Procedimiento BT(x: real; D, MaxD: entero); comience si D = MaxD entonces escribaln(x) de lo contrario comience BT(x – 1, D + 1, MaxD); BT(x + 1, D + 1, MáxD); fin; fin;

2. Ouroboros: una serpiente que devora su propia cola (Fig. 14) cuando está desplegada tiene una longitud l, diámetro alrededor de la cabeza D, espesor de la pared abdominal d. Determine cuánta cola puede meter dentro y en cuántas capas se colocará la cola después de eso.

Arroz. 14. Ouroboros ampliado.

3. Para el árbol de la Fig. 10a indican la secuencia de nodos visitantes en orden transversal directo, inverso y final.

4. Representa gráficamente el árbol definido mediante corchetes anidados: (A(B(C, D), E), F, G).

5. Representa gráficamente el árbol de sintaxis de la siguiente expresión aritmética:

Escribe esta expresión en notación polaca inversa.

6. Para el siguiente gráfico (Fig. 15), escriba la matriz de adyacencia y la matriz de incidencia.

Tareas

1. Habiendo calculado el factorial un número suficientemente grande de veces (un millón o más), compare la efectividad de los algoritmos recursivos e iterativos. ¿Cuánto diferirá el tiempo de ejecución y cómo dependerá esta relación del número cuyo factorial se esté calculando?

2. Escriba una función recursiva que verifique si los paréntesis están colocados correctamente en una cadena. Si el arreglo es correcto, se cumplen las siguientes condiciones:

(a) el número de paréntesis de apertura y cierre es igual.
(b) dentro de cualquier par hay un corchete de apertura - cierre correspondiente, los corchetes están colocados correctamente.

Ejemplos de colocación incorrecta:)(, ())(, ())((), etc.

3. La línea puede contener corchetes y corchetes. Cada corchete de apertura tiene su correspondiente corchete de cierre del mismo tipo (redondo - redondo, cuadrado - cuadrado). Escribe una función recursiva que verifique si los paréntesis están colocados correctamente en este caso.

Ejemplo de colocación incorrecta: ([)].

4. El número de estructuras de corchetes regulares de longitud 6 es 5: ()()(), (())(), ()(()), ((())), (()()).
Escriba un programa recursivo para generar todas las estructuras de corchetes regulares de longitud 2 norte.

Nota: Estructura de paréntesis correcta de longitud mínima "()". Las estructuras de mayor longitud se obtienen a partir de estructuras de menor longitud de dos formas:

a) si la estructura más pequeña se incluye entre paréntesis,
(b) si dos estructuras más pequeñas se escriben secuencialmente.

5. Cree un procedimiento que imprima todas las permutaciones posibles para números enteros del 1 al N.

6. Cree un procedimiento que imprima todos los subconjuntos del conjunto (1, 2, ..., N).

7. Cree un procedimiento que imprima todas las representaciones posibles del número natural N como la suma de otros números naturales.

8. Cree una función que calcule la suma de los elementos de la matriz usando el siguiente algoritmo: la matriz se divide por la mitad, las sumas de los elementos de cada mitad se calculan y suman. La suma de los elementos de la mitad de la matriz se calcula utilizando el mismo algoritmo, es decir, nuevamente dividiendo por la mitad. Las divisiones ocurren hasta que las piezas resultantes de la matriz contienen un elemento cada una y, en consecuencia, calcular la suma se vuelve trivial.

Comentario: Este algoritmo es una alternativa. En el caso de matrices de valor real, normalmente permite errores de redondeo más pequeños.

10. Cree un procedimiento que dibuje la curva de Koch (Figura 12).

11. Reproduce la figura. 16. En la figura, en cada iteración siguiente el círculo es 2,5 veces más pequeño (este coeficiente se puede convertir en un parámetro).

Literatura

1. D. Knuth. El arte de la programación informática. v. 1. (sección 2.3. “Árboles”).
2. N. Wirth. Algoritmos y estructuras de datos.