Confidence interval is a formula for calculating a physicist. Construction of the confidence interval for the mathematical expectation of the general population. Confidence Interval Method
Last Updated: March 3, 2020
Example fileLet us construct a confidence interval in MS EXCEL to estimate the mean value of the distribution in the case of known importance variance.
Of course the choice level of trust completely depends on the problem being solved. Thus, the degree of confidence of the air passenger in the reliability of the aircraft, undoubtedly, should be higher than the degree of confidence of the buyer in the reliability of the light bulb.
Statement of the problem
Suppose that from the general population having taken sample size n. It is assumed that standard deviation this distribution is known. It is necessary on the basis of this sampling evaluate the unknown mean distribution(μ,) and construct the corresponding two-sidedconfidence interval .
Point estimate
As is known from, statistics(we denote it X Wed) is an unbiased estimate of the mean this the general population and has the distribution N (μ; σ 2 / n).
Note : What to do if you need to build confidence interval in the case of a distribution that is notnormal? In this case, it comes to the rescue, which says that with a sufficiently large size sampling n from distribution not beingnormal , sample distribution of statistics X av will approximately correspond normal distribution with parameters N (μ; σ 2 / n).
So, point estimatemiddledistribution values we have - this sample mean, i.e. X Wed... Now let's get down to confidence interval.
Plotting a Confidence Interval
Usually, knowing the distribution and its parameters, we can calculate the probability that the random variable will take a value from the interval we specified. Now let's do the opposite: find the interval in which the random variable will fall with a given probability. For example, from the properties normal distribution it is known that with a probability of 95%, a random variable distributed over normal law, will fall within an interval of approximately +/- 2 from mean value(see article about). This interval will serve as a prototype for us confidence interval .
Now let's figure out if we know the distribution , to calculate this interval? To answer the question, we must indicate the shape of the distribution and its parameters.
We know the distribution form - it is normal distribution(recall that we are talking about sample distributionstatisticsX Wed).
We do not know the parameter μ (it just needs to be estimated using confidence interval), but we have his estimate X Wed, calculated based on sampling, which can be used.
The second parameter is standard deviation of the sample meanwe will consider it known, it is equal to σ / √n.
Because we do not know μ, then we will construct the interval +/- 2 standard deviations not from mean value, and from its known estimate X Wed... Those. when calculating confidence interval we will NOT assume that X Wed falls within +/- 2 standard deviations from μ with a probability of 95%, and we will assume that the interval +/- 2 standard deviations from X Wed with a probability of 95% will cover μ - average of the general population, from which it is taken sample... These two statements are equivalent, but the second statement allows us to construct confidence interval .
In addition, we clarify the interval: a random variable distributed over normal law, with a probability of 95% falls within the interval +/- 1.960 standard deviations, not +/- 2 standard deviations... This can be calculated using the formula = NORM.ST.OBR ((1 + 0.95) / 2), cm. example file Sheet Spacing .

We can now formulate a probabilistic statement that will serve us to form confidence interval: “The probability that population average is from average sample within 1,960 " standard deviations of the sample mean " is equal to 95% ".
The probability value mentioned in the statement has a special name which is associated with significance level α (alpha) by a simple expression trust level = 1 -α . In our case significance level α =1-0,95=0,05 .
Now, based on this probabilistic statement, we write down an expression for calculating confidence interval :

where Z α / 2 – standardnormal distribution(such a value of the random variable z , what P (z >= Z α / 2 ) = α / 2).
Note : Upper α / 2-quantile determines the width confidence interval v standard deviationssample mean. Upper α / 2-quantile standardnormal distribution always greater than 0, which is very convenient.
In our case, at α = 0.05, upper α / 2-quantile is equal to 1.960. For other significance levels α (10%; 1%) upper α / 2-quantileZ α / 2 can be calculated using the formula = STANDARD ST.OBR (1-α / 2) or if known trust level , = NORM.ST.OBR ((1 + level of trust) / 2) .
Usually when building confidence intervals for estimating the mean only use upper α /2- quantile and don't use lower α /2- quantile... This is possible because standardnormal distribution symmetrically about the x-axis ( its distribution density symmetrical with respect to average, i.e. 0) . Therefore, there is no need to calculate lower α / 2-quantile(it is simply called α / 2-quantile), because it is equal upper α /2- quantile with a minus sign.
Recall that, despite the shape of the distribution of the quantity x, the corresponding random variable X Wed distributed approximatelyfine N (μ; σ 2 / n) (see article about). Therefore, in the general case, the above expression for confidence interval is only approximate. If the quantity x is distributed over normal law N (μ; σ 2 / n), then the expression for confidence interval is accurate.
Confidence interval calculation in MS EXCEL
Let's solve the problem. Response time electronic component to the input signal is an important characteristic of the device. The engineer wants to plot a confidence interval for the average response time at a 95% confidence level. The engineer knows from previous experience that the standard deviation of the response time is 8ms. It is known that the engineer made 25 measurements to estimate the response time, the average value was 78 ms.
Solution: An engineer wants to know the response time of an electronic device, but he understands that the response time is not a fixed, but a random variable that has its own distribution. So the best he can count on is to determine the parameters and shape of this distribution.
Unfortunately, from the problem statement, we do not know the shape of the response time distribution (it does not have to be normal). , this distribution is also unknown. Known only for him standard deviationσ = 8. Therefore, while we cannot calculate the probabilities and build confidence interval .
However, despite the fact that we do not know the distribution timeseparate response, we know that according to CPT , sample distributionaverage response time is approximately normal(we will assume that the conditions CPT are performed because the size sampling large enough (n = 25)) .
Moreover, the average of this distribution is average the distribution of a single response, i.e. μ. A standard deviation of this distribution (σ / √n) can be calculated by the formula = 8 / ROOT (25).
It is also known that the engineer received point estimate parameter μ equal to 78 msec (X cf.). Therefore, now we can calculate the probabilities, since we know the distribution form ( normal) and its parameters (X cf and σ / √n).
The engineer wants to know expected valueμ of the response time distribution. As mentioned above, this μ is equal to the mathematical expectation of the sample distribution of the mean response time... If we use normal distribution N (X cf; σ / √n), then the desired μ will be in the range +/- 2 * σ / √n with a probability of about 95%.
Significance level is equal to 1-0.95 = 0.05.
Finally, find the left and right border confidence interval... Left border: = 78-STANDARD ST.OBR (1-0.05 / 2) * 8 / ROOT (25) = 74,864 Right border: = 78 + NORM.ST.OBR (1-0.05 / 2) * 8 / ROOT (25) = 81.136
Left border: = NORM.OBR (0.05 / 2; 78; 8 / ROOT (25)) Right border: = NORM.INV (1-0.05 / 2; 78; 8 / ROOT (25))
Answer : confidence interval at confidence level 95% and σ =8 ms is equal to 78 +/- 3.136 msec.
V example file on Sigma worksheet a form for calculation and construction is known bilateralconfidence interval for arbitrary samples with a given σ and level of significance .

CONFIDENCE.NORM () function
If the values sampling are in the range B20: B79 , a significance level equal to 0.05; then the MS EXCEL formula: = AVERAGE (B20: B79) -TRUST.NORM (0.05, σ, COUNT (B20: B79)) will return the left border confidence interval .
The same border can be calculated using the formula: = AVERAGE (B20: B79) -NORM.ST.INV (1-0.05 / 2) * σ / ROOT (COUNT (B20: B79))
Note: The CONFIDENCE.NORM () function appeared in MS EXCEL 2010. In earlier versions of MS EXCEL, the CONFIDENCE () function was used.
In the previous subsections, we considered the question of estimating an unknown parameter a one number. This estimate is called "point". In a number of tasks, it is required not only to find for the parameter a a suitable numerical value, but also evaluate its accuracy and reliability. You want to know what errors a parameter replacement can lead to a its point estimate a and with what degree of certainty can we expect these errors to stay within known limits?
Problems of this kind are especially relevant for a small number of observations, when the point estimate and in to a large extent, it is accidental and the approximate replacement of a by a can lead to serious errors.
To give an idea of the accuracy and reliability of the assessment a,
in mathematical statistics so-called confidence intervals and confidence probabilities are used.
Let for the parameter a from experience unbiased estimate a. We want to evaluate the possible error in this case. Let us assign some sufficiently large probability p (for example, p = 0.9, 0.95 or 0.99) such that an event with a probability p can be considered practically reliable, and find such a value s for which
Then the range of practically possible values of the error arising when replacing a on a, will be ± s; large in absolute value errors will appear only with a small probability a = 1 - p. Let's rewrite (14.3.1) as:
Equality (14.3.2) means that with probability p the unknown value of the parameter a falls within the interval
In this case, one circumstance should be noted. Earlier, we have repeatedly considered the probability of a random variable falling into a given non-random interval. Here the situation is different: the quantity a not accidental, but the interval / p is random. Randomly its position on the abscissa axis, determined by its center a; the length of the interval 2s is also random in general, since the value of s is calculated, as a rule, from experimental data. Therefore, in this case, it would be better to interpret the value of p not as the probability of "hitting" the point a into the interval / p, and as the probability that the random interval / p will cover the point a(fig. 14.3.1).

Rice. 14.3.1
The probability p is usually called confidence level, and the interval / p is confidence interval. Interval boundaries If. a x = a- s and a 2 = a + but called confidence limits.
Let us give one more interpretation of the concept of a confidence interval: it can be considered as an interval of parameter values a, compatible with experimental data and not contradicting them. Indeed, if we agree to consider an event with probability a = 1-p practically impossible, then those values of the parameter a for which a - a> s, must be recognized as contradicting the experimental data, and those for which | a - a a t na 2.
Let for the parameter a there is an unbiased estimate a. If we knew the distribution law of the quantity a, the problem of finding the confidence interval would be very simple: it would be enough to find such a value of s for which
![]()
The difficulty is that the distribution law of the estimate a depends on the distribution law of the quantity X and, therefore, on its unknown parameters (in particular, on the parameter itself a).
To get around this difficulty, the following rough approximation can be applied: replace the unknown parameters in the expression for s with their point estimates. With a relatively large number of experiments NS(about 20 ... 30) this technique usually gives results satisfactory in terms of accuracy.
As an example, consider the problem of the confidence interval for the mathematical expectation.
Let it be produced NS X, whose characteristics are the mathematical expectation T and variance D- unknown. For these parameters, the following estimates were obtained:

It is required to construct the confidence interval / p, corresponding to the confidence probability p, for the mathematical expectation T magnitudes X.
When solving this problem, we will use the fact that the quantity T represents the amount NS independent identically distributed random variables X h and according to the central limit theorem for sufficiently large NS its distribution law is close to normal. In practice, even with a relatively small number of terms (about 10 ... 20), the distribution law of the sum can be approximately considered normal. We will proceed from the fact that the quantity T distributed according to the normal law. The characteristics of this law - mathematical expectation and variance - are equal, respectively T and
(see chapter 13 subsection 13.3). Suppose that the quantity D we know and find such a value Ep, for which
Applying formula (6.3.5) in Chapter 6, we express the probability on the left-hand side of (14.3.5) in terms of the normal distribution function
where is the standard deviation of the estimate T.
From the equation

we find the value of Sp: 
where arg Ф * (х) is the inverse function of Ф * (NS), those. such a value of the argument for which the normal distribution function is equal to NS.
Dispersion D, through which the value is expressed a 1P, we do not know exactly; as its approximate value, you can use the estimate D(14.3.4) and put approximately:

Thus, the problem of constructing a confidence interval has been approximately solved, which is equal to:
where gp is defined by formula (14.3.7).
In order to avoid inverse interpolation in the tables of the function Ф * (л) when calculating s p, it is convenient to compile a special table (Table 14.3.1), which gives the values of the quantity
depending on the p. The quantity (p determines for the normal law the number of standard deviations that must be postponed to the right and left of the center of scattering in order for the probability of hitting the resulting area to be equal to p.
Through the value of 7 p, the confidence interval is expressed as:

Table 14.3.1
Example 1. Conducted 20 experiments on the value X; the results are shown in table. 14.3.2.
Table 14.3.2
It is required to find an estimate of for the mathematical expectation of the quantity X and build a confidence interval corresponding to a confidence level of p = 0.8.
Solution. We have:

Having chosen as the origin l: = 10, according to the third formula (14.2.14) we find the unbiased estimate D :

According to the table. 14.3,1 find ![]()
![]()
Confidence limits:

Confidence interval:
![]()
Parameter values T, lying in this interval are consistent with the experimental data given in table. 14.3.2.
The confidence interval for the variance can be constructed in a similar way.
Let it be produced NS independent experiments on a random variable X with unknown parameters from and A, and for the variance D the unbiased estimate is obtained:


It is required to roughly construct the confidence interval for the variance.
From formula (14.3.11) it is seen that the quantity D represents
the sum NS random variables of the form. These quantities are not
independent, since any of them includes the quantity T, dependent on everyone else. However, it can be shown that with increasing NS the distribution law of their sum is also close to normal. Practically at NS= 20 ... 30 it can already be considered normal.
Let us assume that this is so, and find the characteristics of this law: mathematical expectation and variance. Since the score D- unbiased, then M [D] = D.
Calculating variance D D is associated with relatively complex calculations, so we give its expression without output:
where q 4 is the fourth central moment of the quantity X.
To use this expression, you need to substitute in it the values \ u200b \ u200b4 and D(at least approximate). Instead of D you can use his estimate D. In principle, the fourth central moment can also be replaced by an estimate, for example, by a value of the form:

but such a replacement will give an extremely low accuracy, since in general, with a limited number of experiments, high-order moments are determined with large errors. However, in practice it often happens that the form of the distribution law of the quantity X known in advance: only its parameters are unknown. Then you can try to express q 4 in terms of D.
Let us take the most frequent case when the quantity X distributed according to the normal law. Then its fourth central moment is expressed in terms of variance (see Chapter 6 Subsection 6.2);
![]()
and formula (14.3.12) gives  or
or
Replacing in (14.3.14) the unknown D his assessment D, we get: whence 
The moment c 4 can be expressed in terms of D also in some other cases, when the distribution of the quantity X is not normal, but its appearance is known. For example, for the law of uniform density (see Chapter 5) we have: 
where (a, P) is the interval at which the law is specified.
Hence,
![]()
By the formula (14.3.12) we get:  whence we find approximately
whence we find approximately
In cases where the form of the distribution law of 26 is unknown, it is still recommended to use formula (14.3.16) when roughly estimating the value of a /), unless there are special reasons to believe that this law is very different from the normal (has a noticeable positive or negative excess) ...
If the approximate value of a /) is obtained in one way or another, then it is possible to construct a confidence interval for the variance in the same way as we built it for the mathematical expectation:
where the value, depending on the given probability p, is found according to the table. 14.3.1.
Example 2. Find an approximately 80% confidence interval for the variance of a random variable X under the conditions of Example 1, if it is known that the quantity X distributed according to a law close to normal.
Solution. The value remains the same as in table. 14.3.1:
![]()
According to the formula (14.3.16)

Using the formula (14.3.18), we find the confidence interval:
![]()
The corresponding range of values of the standard deviation: (0.21; 0.29).
14.4. Exact methods for constructing confidence intervals for the parameters of a random variable distributed according to the normal law
In the previous subsection, we looked at roughly approximate methods for constructing confidence intervals for expectation and variance. Here we will give an idea of the exact methods for solving the same problem. We emphasize that in order to accurately find the confidence intervals, it is absolutely necessary to know in advance the form of the distribution law of the quantity X, while for the application of approximate methods this is not necessary.
The idea behind accurate methods for constructing confidence intervals is as follows. Any confidence interval is found from the condition expressing the probability of the fulfillment of some inequalities, which include the estimate of interest to us a. Estimation distribution law a in the general case depends on the unknown parameters of the quantity X. However, sometimes it is possible to pass in inequalities from a random variable a to some other function of observed values X n X 2, ..., X p. whose distribution law does not depend on unknown parameters, but depends only on the number of experiments and on the form of the distribution law for the quantity X. Random variables of this kind play an important role in mathematical statistics; they have been studied in most detail for the case of the normal distribution of the quantity X.
For example, it was proved that for a normal distribution of the quantity X random value

obeys the so-called Student distribution law with NS- 1 degrees of freedom; the density of this law has the form

where Г (х) is the known gamma function:

It was also proved that the random variable
has a "distribution% 2" with NS- 1 degrees of freedom (see Chapter 7), the density of which is expressed by the formula

Without dwelling on the derivations of distributions (14.4.2) and (14.4.4), we show how they can be applied when constructing confidence intervals for the parameters ty D.
Let it be produced NS independent experiments on a random variable X, distributed according to the normal law with unknown parameters thio. For these parameters, the estimates were obtained

It is required to construct confidence intervals for both parameters corresponding to the confidence probability p.
Let us first construct the confidence interval for the mathematical expectation. Naturally, this interval is taken symmetric with respect to T; denote by s p half the length of the interval. The value s p must be chosen so that the condition
Let's try to pass on the left-hand side of equality (14.4.5) from the random variable T to a random variable T, distributed according to Student's law. To do this, we multiply both sides of the inequality | m-w? |
by a positive value:  or, using the notation (14.4.1),
or, using the notation (14.4.1),

Let us find a number / p such that the value / p is found from the condition

It is seen from formula (14.4.2) that (1) is an even function, therefore (14.4.8) gives 
Equality (14.4.9) determines the value of / p depending on p. If you have at your disposal a table of values of the integral

then the value of / p can be found by reverse interpolation in the table. However, it is more convenient to compile a table of / p values in advance. Such a table is given in the appendix (Table 5). This table shows the values depending on the confidence probability p and the number of degrees of freedom NS- 1. Having determined / p according to the table. 5 and assuming 
we will find half the width of the confidence interval / p and the interval itself
Example 1. Made 5 independent experiments on a random variable X, normally distributed with unknown parameters T and about. The results of the experiments are shown in table. 14.4.1.
Table 14.4.1
Find a grade T for the mathematical expectation and construct a 90% confidence interval / p for it (i.e., the interval corresponding to the confidence probability p = 0.9).
Solution. We have:
![]()
According to table 5 applications for NS - 1 = 4 and p = 0.9 we find ![]() where
where 
The confidence interval will be
Example 2. For the conditions of example 1 of subsection 14.3, assuming the value X distributed normally, find the exact confidence interval.
Solution. According to table 5, we find applications for NS - 1 = 19ir =
0.8 / p = 1.328; from here 
Comparing with the solution of example 1 of subsection 14.3 (e p = 0.072), we are convinced that the discrepancy is very insignificant. If we keep the accuracy to the second decimal place, then the confidence intervals found by exact and approximate methods coincide:
![]()
Let's move on to constructing a confidence interval for the variance. Consider the unbiased variance estimate

and express the random variable D through the value V(14.4.3) having a distribution x 2 (14.4.4):

Knowing the distribution law of the quantity V, one can find the interval / (1, in which it falls with a given probability p.
Distribution law k n _ x (v) quantity I 7 has the form shown in Fig. 14.4.1.

Rice. 14.4.1
The question arises: how to choose the interval / p? If the distribution law of the quantity V was symmetric (like the normal law or the Student's distribution), it would be natural to take the interval / p symmetric with respect to the mathematical expectation. In this case, the law k n _ x (v) asymmetrical. Let us agree to choose the interval / p so that the probabilities of the output of the quantity V outside the interval to the right and to the left (shaded areas in Fig. 14.4.1) were the same and equal

To construct an interval / p with this property, we will use table. 4 appendices: it lists numbers y) such that
![]()
for the quantity V, having x 2 -distribution with r degrees of freedom. In our case r = n- 1. Let us fix r = n- 1 and find in the corresponding line of the table. 4 two meanings x 2 - one corresponding to probability the other - probabilities Let us denote these
meaning at 2 and xl? The interval has at 2, his left, and y ~ right end.
Now let us find the desired confidence interval / | for the variance with boundaries D, and D 2, which covers the point D with probability p: ![]()
Let us construct such an interval / (, = (?> B A), which covers the point D if and only if the quantity V falls into the interval / p. Let us show that the interval

satisfies this condition. Indeed, the inequalities  are equivalent to inequalities
are equivalent to inequalities
![]()
and these inequalities are satisfied with probability p. Thus, the confidence interval for the variance is found and is expressed by the formula (14.4.13).
Example 3. Find the confidence interval for the variance under the conditions of example 2 in subsection 14.3, if it is known that the value X distributed normally.
Solution. We have ![]() ... According to table 4 of the appendix
... According to table 4 of the appendix
we find at r = n - 1 = 19

Using the formula (14.4.13), we find the confidence interval for the variance ![]()
Corresponding interval for standard deviation: (0.21; 0.32). This interval only slightly exceeds the interval (0.21; 0.29) obtained in example 2 of subsection 14.3 by an approximate method.
- Figure 14.3.1 considers a confidence interval that is symmetric about a. In general, as we will see later, this is optional.
Confidence interval(CI; in English, confidence interval - CI) obtained in a study with a sample gives a measure of the accuracy (or uncertainty) of the study results in order to draw conclusions about the population of all such patients (general population). The correct definition of 95% CI can be formulated as follows: 95% of such intervals will contain the true value in the population. This interpretation is somewhat less accurate: CI is the range of values within which one can be 95% sure that it contains the true value. When using CIs, the emphasis is on quantifying the effect, as opposed to the P value that is obtained by testing for statistical significance. The P value does not measure any quantity, but rather serves as a measure of the strength of the evidence against the null hypothesis of "no effect." The P value by itself does not tell us anything about the magnitude of the difference, or even about its direction. Therefore, independent values of P are absolutely uninformative in articles or abstracts. In contrast, CI indicates both the amount of effect of immediate interest, such as the usefulness of a treatment, and the strength of the evidence. Therefore, JI is directly related to the practice of EBM.
Assessment approach to statistical analysis, illustrated by the CI, is aimed at measuring the amount of the effect of interest (sensitivity of the diagnostic test, the frequency of predicted cases, reduction of the relative risk in treatment, etc.), as well as measuring the uncertainty in this effect. Most often, CI is the range of values on both sides of the estimate, in which the true value is likely to lie, and you can be 95% sure of this. The agreement to use the 95% probability arbitrarily, as well as the P value<0,05 для оценки статистической значимости, и авторы иногда используют 90% или 99% ДИ. Заметим, что слово «интервал» означает диапазон величин и поэтому стоит в единственном числе. Две величины, которые ограничивают интервал, называются «доверительными пределами».
The CI is based on the idea that the same study performed on other patient samples would not lead to identical results, but that their results would be distributed around a true but unknown value. In other words, the CI describes this as “sample-dependent variability”. The CI does not reflect additional uncertainty due to other causes; in particular, it does not include the effects of selective patient loss in tracking, poor compliance or inaccurate outcome measurement, lack of blinding, and so on. CI thus always underestimates the total amount of uncertainty.
Calculating the Confidence Interval
Table A1.1. Standard errors and confidence intervals for some clinical measurements
Typically, the CI is calculated from an observed estimate of a quantitative measure, such as the difference (d) between two proportions, and a standard error (SE) in the estimate of this difference. The approximate 95% CI thus obtained is d ± 1.96 SE. The formula changes according to the nature of the outcome measure and the scope of the CI. For example, in a randomized, placebo-controlled trial of acellular pertussis vaccine, 72 of 1,670 (4.3%) infants who received the vaccine developed pertussis and 240 of 1,665 (14.4%) controls. The difference in percentage, known as absolute risk reduction, is 10.1%. The SE of this difference is 0.99%. Accordingly, the 95% CI is 10.1% + 1.96 x 0.99%, i.e. from 8.2 to 12.0.
Despite different philosophical approaches, CI and statistical significance tests are closely related mathematically.
Thus, the P value is "significant", i.e. R<0,05 соответствует 95% ДИ, который исключает величину эффекта, указывающую на отсутствие различия. Например, для различия между двумя средними пропорциями это ноль, а для относительного риска или отношения шансов - единица. При некоторых обстоятельствах эти два подхода могут быть не совсем эквивалентны. Преобладающая точка зрения: оценка с помощью ДИ - предпочтительный подход к суммированию результатов исследования, но ДИ и величина Р взаимодополняющи, и во многих статьях используются оба способа представления результатов.
The uncertainty (uncertainty) of the estimate, expressed in CI, is largely related to the square root of the sample size. Small samples provide less information than large ones, and the CI is correspondingly wider in the smaller sample. For example, an article comparing the characteristics of three tests that are used to diagnose Helicobacter pylori infection reported a sensitivity of 95.8% of the urea breath test (95% CI 75-100). While the number of 95.8% looks impressive, a small sample of 24 adult patients with I. pylori means that there is significant uncertainty in this estimate, as shown by the broad CI. Indeed, the lower limit of 75% is much lower than the estimate of 95.8%. If the same sensitivity was observed in a sample of 240 people, then the 95% CI would be 92.5-98.0, giving more guarantees that the test is highly sensitive.
In randomized controlled trials (RCTs), non-significant results (i.e., those with P> 0.05) are particularly susceptible to misinterpretation. The CI is particularly useful here because it shows how consistent the results are with the clinically beneficial true effect. For example, in an RCT comparing suture versus stapling anastomosis to the colon, wound infection developed in 10.9% and 13.5% of patients, respectively (P = 0.30). The 95% CI for this difference is 2.6% (-2 to +8). Even in this study of 652 patients, the likelihood remains that there is a modest difference in the incidence of infections resulting from the two procedures. The less research, the more uncertainty. Sung et al. performed an RCT to compare octreotide infusion versus emergency sclerotherapy for acute variceal bleeding in 100 patients. In the octreotide group, the bleeding arrest rate was 84%; in the sclerotherapy group - 90%, which gives P = 0.56. Note that the rates of ongoing bleeding are similar to those of wound infection in the mentioned study. In this case, however, the 95% CI for the difference between interventions is 6% (-7 to +19). This interval is quite wide compared to the 5% difference that would be of clinical interest. It is clear that the study does not rule out a significant difference in effectiveness. Therefore, the authors' conclusion “octreotide infusion and sclerotherapy are equally effective in treating varicose vein bleeding” is definitely not valid. In cases like this, where, as here, the 95% CI for absolute risk reduction (ARR) includes zero, the CI for number needed to treat (NNT) is rather difficult to interpret. ... The NPLP and its CI are derived from the reciprocal of the ACP (multiplied by 100 if given as percentages). Here we get BPHP = 100: 6 = 16.6 with a 95% CI of -14.3 to 5.3. As you can see from the footnote "d" in the table. A1.1, this CI includes the BPHP values from 5.3 to infinity and the BPHP values from 14.3 to infinity.
CIs can be constructed for most commonly used statistical estimates or comparisons. For RCTs, it includes the difference between mean proportions, relative risks, odds ratios, and NPP. Similarly, CIs can be obtained for all major estimates made in studies of the accuracy of diagnostic tests - sensitivity, specificity, predictive value of a positive result (all of which are simple proportions), and likelihood ratios - estimates obtained in meta-analyzes and comparison-with-control studies. A computer program for personal computers that covers many of these uses of ID is available with the second edition of Statistics with Confidence. Macros for calculating CI for proportions are available free of charge for Excel and the statistical programs SPSS and Minitab at http://www.uwcm.ac.uk/study/medicine/epidemiology_statistics / research / statistics / proportions, htm.
Multiple evaluations of the treatment effect
While CIs are desirable for the primary study results, they are not required for all results. The CI deals with clinically relevant comparisons. For example, when comparing two groups, the CI that is built to distinguish between the groups, as shown in the examples above, is correct, and not the CI that can be built for the assessment in each group. Not only is it useless to provide separate CIs for ratings in each group, this representation can be misleading. Likewise, the correct approach when comparing treatment efficacy in different subgroups is to compare two (or more) subgroups directly. It is incorrect to assume that treatment is effective in only one subgroup if its CI excludes no effect and others do not. CIs are also useful when comparing results across multiple subgroups. In fig. A 1.1 shows the relative risk of eclampsia in women with preeclampsia in a subgroup of women from a placebo-controlled RCT of magnesium sulfate.
Rice. A1.2. The forest plot shows the results of 11 randomized clinical trials of bovine rotavirus vaccine for the prevention of diarrhea versus placebo. In assessing the relative risk of diarrhea, a 95% confidence interval was used. The size of the black square is proportional to the amount of information. In addition, the cumulative treatment efficacy score and the 95% confidence interval (denoted by a diamond) are shown. The meta-analysis used a random effects model that exceeds some of the pre-established ones; for example, it could be the size used in calculating the sample size. For a more stringent criterion, the entire CI range should show benefits in excess of a predetermined minimum.
We have already discussed the error in which the lack of statistical significance is taken as an indication that two treatments are equally effective. It is equally important not to equate statistical significance with clinical significance. Clinical importance can be inferred when the outcome is statistically significant and the magnitude of the assessment of treatment efficacy
Research can show whether results are statistically significant and which are clinically important and which are not. In fig. A1.2 shows the results of four tests for which the entire CI<1, т.е. их результаты статистически значимы при Р <0,05 , . После высказанного предположения о том, что клинически важным различием было бы сокращение риска диареи на 20% (ОР = 0,8), все эти испытания показали клинически значимую оценку сокращения риска, и лишь в исследовании Treanor весь 95% ДИ меньше этой величины. Два других РКИ показали клинически важные результаты, которые не были статистически значимыми. Обратите внимание, что в трёх испытаниях точечные оценки эффективности лечения были почти идентичны, но ширина ДИ различалась (отражает размер выборки). Таким образом, по отдельности доказательная сила этих РКИ различна.
Confidence interval for expected value - this is such an interval calculated from the data, which with a known probability contains the mathematical expectation of the general population. A natural estimate for the mathematical expectation is the arithmetic mean of its observed values. Therefore, further in the lesson, we will use the terms "average", "mean value". In the tasks of calculating the confidence interval, an answer of the type "The confidence interval of the mean [the value in a particular problem] is from [lower value] to [higher value]" is most often required. With the help of the confidence interval, it is possible to estimate not only the average values, but also the specific weight of a particular feature of the general population. The mean values, variance, standard deviation and error, through which we will come to new definitions and formulas, are disassembled in the lesson Sample and population characteristics .
Point and interval estimates of the mean
If the average value of the general population is estimated by a number (point), then the estimate of the unknown average value of the general population is taken to be the specific average, which is calculated from the sample of observations. In this case, the value of the sample mean - a random variable - does not coincide with the average value of the general population. Therefore, when specifying the mean value of the sample, it is necessary to indicate the sampling error at the same time. As a measure of sampling error, the standard error is used, which is expressed in the same units as the mean. Therefore, the following notation is often used:.
If the estimate of the mean is required to be associated with a certain probability, then the parameter of interest for the general population must be estimated not by one number, but by an interval. The confidence interval is the interval in which, with a certain probability P the value of the estimated indicator of the general population is found. Confidence interval, in which the probability P = 1 - α a random variable is found, calculated as follows:
![]() ,
,
α = 1 - P, which can be found in the appendix to almost any book on statistics.
In practice, the population mean and variance are not known, so the population variance is replaced by the sample variance, and the population mean is replaced by the sample mean. Thus, the confidence interval in most cases is calculated as follows:
![]() .
.
The confidence interval formula can be used to estimate the population mean if
- the standard deviation of the general population is known;
- or the standard deviation of the population is not known, but the sample size is greater than 30.
The sample mean is the unbiased estimate of the population mean. In turn, the sample variance  is not an unbiased estimate of population variance. To obtain an unbiased estimate of the variance of the general population in the sample variance formula, the sample size n should be replaced with n-1.
is not an unbiased estimate of population variance. To obtain an unbiased estimate of the variance of the general population in the sample variance formula, the sample size n should be replaced with n-1.
Example 1. Collected information from 100 randomly selected cafes in a city that the average number of employees in them is 10.5 with a standard deviation of 4.6. Determine the confidence interval of 95% of the number of cafe workers.
where is the critical value of the standard normal distribution for the significance level α = 0,05 .
Thus, the 95% confidence interval for the average number of cafe workers ranged from 9.6 to 11.4.
Example 2. For a random sample from a general population of 64 observations, the following total values were calculated:
the sum of the values in the observations,
the sum of the squares of the deviation of the values from the mean ![]() .
.
Calculate the 95% confidence interval for the expectation.
calculate the standard deviation:
 ,
,
calculate the average value:
![]() .
.
Substitute the values into the expression for the confidence interval:
where is the critical value of the standard normal distribution for the significance level α = 0,05 .
We get:
Thus, the 95% confidence interval for the mathematical expectation of this sample ranged from 7.484 to 11.266.
Example 3. For a random sample from a general population of 100 observations, a mean of 15.2 and a standard deviation of 3.2 were calculated. Calculate the 95% confidence interval for the expectation, then the 99% confidence interval. If the sample size and its variation remain unchanged, and the confidence coefficient increases, will the confidence interval narrow or widen?
Substitute these values into the expression for the confidence interval:
where is the critical value of the standard normal distribution for the significance level α = 0,05 .
We get:
![]() .
.
Thus, the 95% confidence interval for the mean of this sample ranged from 14.57 to 15.82.
Once again, we substitute these values into the expression for the confidence interval:
where is the critical value of the standard normal distribution for the significance level α = 0,01 .
We get:
![]() .
.
Thus, the 99% confidence interval for the mean of this sample ranged from 14.37 to 16.02.
As you can see, with an increase in the confidence coefficient, the critical value of the standard normal distribution also increases, and, therefore, the start and end points of the interval are located further from the mean, and, thus, the confidence interval for the mathematical expectation increases.
Point and interval estimates of specific gravity
The specific weight of some feature of the sample can be interpreted as a point estimate of the specific weight p the same feature in the general population. If this value needs to be related to probability, then the confidence interval of the specific gravity should be calculated p trait in the general population with a probability P = 1 - α :
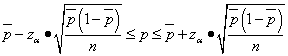 .
.
Example 4. There are two candidates in some city A and B run for mayor. 200 residents of the city were randomly interviewed, of which 46% answered that they would vote for the candidate A, 26% - for the candidate B and 28% do not know who they will vote for. Determine the 95% confidence interval for the proportion of city residents who support the candidate A.
Konstantin Krawchik clearly explains what a confidence interval is in medical research and how to use it.
Katren-Stil continues to publish a cycle by Konstantin Kravchik about medical statistics. In the two previous articles, the author has dealt with the explanation of concepts such as and.
Konstantin Kravchik
Analytical mathematician. Specialist in Statistical Research in Medicine and Humanities
Moscow city
Very often in articles on clinical trials, you can find a mysterious phrase: "confidence interval" (95% CI or 95% CI - confidence interval). For example, the article may read: "To assess the significance of the differences, the Student's t-test was used with the calculation of a 95% confidence interval."
What is the value of the "95% confidence interval" and why calculate it?
What is a Confidence Interval? - This is the range in which the true averages are in the population. And what, there are "untrue" average values? In a sense, yes, there are. In we explained that it is impossible to measure the parameter of interest across the entire population, so researchers are content with a limited sample. In this sample (for example, by body weight) there is one average value (a certain weight), by which we judge the average value in the entire general population. However, the average weight in the sample (especially small) is unlikely to coincide with the average weight in the general population. Therefore, it is more correct to calculate and use the range of average values of the general population.
For example, imagine that the 95% CI (95% CI) for hemoglobin is 110 to 122 g / L. This means that with a probability of 95%, the true average hemoglobin value in the general population will be in the range from 110 to 122 g / l. In other words, we do not know the average hemoglobin in the general population, but with a 95% probability we can indicate the range of values for this trait.
The confidence interval is especially relevant for the difference in means between groups, or as it is called, in the size of the effect.
Let's say we were comparing the effectiveness of two iron preparations: one that has been on the market for a long time and one that has just been registered. After the course of therapy, the hemoglobin concentration in the studied groups of patients was assessed, and the statistical program calculated that the difference between the mean values of the two groups with a 95% probability is in the range from 1.72 to 14.36 g / l (Table 1).
Tab. 1. Criterion for independent samples
(compared groups by hemoglobin level)
This should be interpreted as follows: in some of the patients of the general population who take the new drug, hemoglobin will be higher on average by 1.72–14.36 g / l than in those who took the already known drug.
In other words, in the general population, the difference in mean values for hemoglobin in groups with a 95% probability is within these limits. It will be up to the researcher to judge whether this is a lot or a little. The point of all this is that we are working not with one average value, but with a range of values, therefore, we more reliably estimate the difference in parameter between groups.
In statistical packages, at the discretion of the researcher, you can independently narrow or expand the boundaries of the confidence interval. By lowering the likelihood of the confidence interval, we narrow the range of the means. For example, at 90% CI, the range of means (or difference in means) will be narrower than at 95%.
Conversely, increasing the probability to 99% widens the range of values. When comparing groups, the lower limit of the CI may cross the zero mark. For example, if we expanded the confidence interval to 99%, then the boundaries of the interval ranged from –1 to 16 g / L. This means that in the general population there are groups, the difference between the means between which according to the studied attribute is equal to 0 (M = 0).
Using the confidence interval, you can test statistical hypotheses. If the confidence interval crosses zero, then the null hypothesis, which assumes that the groups do not differ in the studied parameter, is correct. An example is described above, when we expanded the boundaries to 99%. Somewhere in the general population, we found groups that did not differ in any way.
95% confidence interval of the difference in hemoglobin, (g / l)

The figure shows the 95% confidence interval of the difference in the mean hemoglobin values between the two groups as a line. The line passes the zero mark, therefore, there is a difference between the means equal to zero, which confirms the null hypothesis that the groups do not differ. The range of difference between groups is from –2 to 5 g / l, which means that hemoglobin can either decrease by 2 g / l or increase by 5 g / l.
The confidence interval is a very important metric. Thanks to him, you can see whether the differences in the groups were really due to the difference in means or due to a large sample, since with a large sample, the chances of finding differences are greater than with a small one.
In practice, it might look like this. We took a sample of 1000 people, measured the level of hemoglobin and found that the confidence interval for the difference in the means was from 1.2 to 1.5 g / L. The level of statistical significance in this case p
We see that the concentration of hemoglobin increased, but almost imperceptibly, therefore, the statistical significance appeared precisely due to the sample size.
The confidence interval can be calculated not only for mean values, but also for proportions (and risk ratios). For example, we are interested in the confidence interval of the proportions of patients who have achieved remission while taking a developed drug. Let us assume that the 95% CI for proportions, that is, for the proportion of such patients, lies in the range of 0.60–0.80. Thus, we can say that our drug has a therapeutic effect from 60 to 80% of cases.



