Givet två rekursiva funktioner f och g. Rekursions- och rekursiva algoritmer. Grundläggande definitioner. Sätt att avbilda träd

En presentation om ämnet "Rekursiva algoritmer" skapades för att förbereda eleverna för Unified State Exam i datavetenskap och IKT. Arbetet undersöker definitionen av rekursion och ger exempel på rekursivt definierade grafiska objekt. Presentationen innehåller metoder för att lösa uppgift nr 11 från utkastet till demoversion av Unified State Exam - 2015 i datavetenskap. Den första metoden innebär att man bygger ett anropsträd, den andra metoden löser problemet med hjälp av substitutionsmetoden. 4 exempel på att lösa uppgifter med båda metoderna beaktas. Följande presentation innehåller 25 övningar för träning med svar från Konstantin Polyakovs hemsida.

Ladda ner:

Förhandsvisning:

För att använda presentationsförhandsvisningar, skapa ett Google-konto och logga in på det: https://accounts.google.com

Bildtexter:

Uppgift nr 11 Unified State Exam (grundnivå, tid - 5 minuter) Rekursiva algoritmer. Författare – Korotun O.V., lärare i datavetenskap, Kommunal läroanstalt ”Gymnasieskolan nr 71”

Vad du behöver veta: Rekursion är definitionen, beskrivningen, skildringen av ett objekt eller en process inom detta objekt eller själva processen, det vill säga en situation när ett objekt är en del av sig själv. Ryska federationens vapen är ett rekursivt definierat grafiskt objekt: i den högra tassen på den dubbelhövdade örnen som avbildas på den, är en spira fastspänd, som kröns med en mindre kopia av vapenskölden. Eftersom det på detta vapen även finns en spira i örnens högra tass, erhålls en oändlig rekursion. Rysslands rekursiva vapen

I programmering är rekursion att anropa en funktion från sig själv, direkt eller genom andra funktioner, till exempel funktion A anropar funktion B och funktion B anropar funktion A. Antalet kapslade anrop till en funktion eller procedur kallas rekursionsdjupet. exempel på rekursion: Om du har en fettfläck på din klänning, oroa dig inte. Oljefläckar tas bort med bensin. Bensinfläckar tas bort med en alkalilösning. Alkaliet tas bort med essens. Gnid spåret av essensen med olja. Tja, du vet redan hur man tar bort oljefläckar!

Exempeluppgift: Givet en rekursiv algoritm: procedur F(n: heltal); börja skrivaln(n); om n

Exempeluppgift: Givet en rekursiv algoritm: procedur F(n: heltal); börja skrivaln(n) ; om n

Exempeluppgift: Givet en rekursiv algoritm: procedur F(n: heltal); börja skrivaln(n); om n Bild 9

Exempeluppgift: Givet en rekursiv algoritm: procedur F(n: heltal); börja skrivaln(n); om n Bild 10

Exempeluppgift: Givet en rekursiv algoritm: procedur F(n: heltal); börja skrivaln(n); om n Bild 11

15 Exempel nr 2: Givet en rekursiv algoritm: procedur F(n: heltal); börja skrivaln(n); om n

Exempel nr 2: Givet en rekursiv algoritm: procedur F(n: heltal); börja skrivaln(n); om n Bild 13

Exempel nr. 3: Givet en rekursiv algoritm: procedur F(n: heltal); begin writeln("*"); om n > 0 börjar då F(n-2); F(n div 2) slutslut ; Hur många asterisker kommer att skrivas ut på skärmen när F(7) anropas? 7 5 3 2 3 1 1 1 1 I det här exemplet visas symbolen * -2 div 2 1 0 -1 0 -1 0 -1 -1 -1 0 0 0 på skärmen istället för värdena för parameter n .

Exempel nr. 3: Givet en rekursiv algoritm: procedur F(n: heltal); börja writeln("*"); om n > 0 börjar då F(n-2); F(n div 2) slutslut ; Hur många asterisker kommer att skrivas ut på skärmen när F(7) anropas? * Genom att räkna antalet "stjärnor" får vi 21 I det här exemplet är det inte värdena för parametern n som visas på skärmen, utan symbolen * * * * * * * * * * * * * * * * * * * * * *

Exempel nr. 3: Givet en rekursiv algoritm: procedur F(n: heltal); börja writeln("*"); om n > 0 börjar då F(n-2); F(n div 2) slutslut ; Hur många asterisker kommer att skrivas ut på skärmen när F(7) anropas? Låt oss lösa problemet utan ett träd. Låt S(n) vara antalet "stjärnor" som kommer att skrivas ut när F(n) anropas. Sedan 1+S(n-2)+ S(n div 2), n>0 1 , n Vi behöver veta S(7). S(7)= 1 +S(5)+ S(3) S(5)= 1 +S(3)+S(2) S(3)= 1 +S(1)+S(1) S( 2)=1+S(0)+S(1)=1+1+S(1)=2+S(1) S(1)= 1+ S(-1)+S(0)=1+ 1+1=3 Omvänt: S(2)=2+3=5 S(3)=1+3+3=7 S(5)=1+7+5=13 S(7)=1+ 13+ 7= 21 S(n)=

Exempel nr 4: procedur F(n: heltal); börja om n Bild 18

Exempel nr 4: procedur F(n: heltal); börja om n Bild 19

Exempel nr 4: procedur F(n: heltal); börja om n

Utbildningsuppgifter

Uppgift 1: Givet en rekursiv algoritm: procedur F(n: heltal); börja writeln("*"); om n > 0 börjar då F(n-2); F(n div 2); F(n div 2); slutände ; Hur många asterisker kommer att skrivas ut på skärmen när F(5) anropas? Svar: 34

Uppgift 2: Givet en rekursiv algoritm: procedur F(n: heltal); börja writeln("*"); om n > 0 börjar då F(n-2); F(n-2); F(n div 2); slutände ; Hur många asterisker kommer att skrivas ut på skärmen när F(6) anropas? Svar: 58

Uppgift 3: Givet en rekursiv algoritm: procedur F(n: heltal); börja writeln("*"); om n > 0 börjar då F(n-3); F(n div 2); slutände ; Hur många asterisker kommer att skrivas ut på skärmen när F(7) anropas? Svar: 15

Uppgift 4: Givet en rekursiv algoritm: procedur F(n: heltal); börja writeln("*"); om n > 0 börjar då F(n-3); F(n-2); F(n div 2); slutände ; Hur många asterisker kommer att skrivas ut på skärmen när F(7) anropas? Svar: 55

Uppgift 5: Givet en rekursiv algoritm: procedur F(n: heltal); börja writeln("*"); om n > 0 börjar då F(n-3); F(n-2); F(n div 2); F(n div 2); slutände ; Hur många asterisker kommer att skrivas ut på skärmen när F(6) anropas? Svar: 97

Uppgift 6: Givet en rekursiv algoritm: procedur F(n: heltal); börja writeln("*"); om n > 0, börja skrivaln("*"); F(n-2); F(n div 2); slutände ; Hur många asterisker kommer att skrivas ut på skärmen när F(7) anropas? Svar: 31

Uppgift 7: Givet en rekursiv algoritm: procedur F(n: heltal); börja writeln("*"); om n > 0, börja skrivaln("*"); F(n-2); F(n div 2); F(n div 2); slutände; Hur många asterisker kommer att skrivas ut på skärmen när F(7) anropas? Svar: 81

Uppgift 8: Givet en rekursiv algoritm: procedur F(n: heltal); börja writeln("*"); om n > 0, börja skrivaln("*"); F(n-2); F(n-2); F(n div 2); slutände; Hur många asterisker kommer att skrivas ut på skärmen när F(6) anropas? Svar: 77

Uppgift 9: Givet en rekursiv algoritm: procedur F(n: heltal); börja om n > 0 börjar då F(n-2); F(n-1); F(n-1); slutet; writeln("*"); slutet ; Hur många asterisker kommer att skrivas ut på skärmen när F(5) anropas? Svar: 148

Uppgift 10: Givet en rekursiv algoritm: procedur F(n: heltal); börja om n > 0, börja skrivaln("*"); F(n-2); F(n-1); F(n-1); slutet; writeln("*"); slutet; Hur många asterisker kommer att skrivas ut på skärmen när F(5) anropas? Svar: 197

Uppgift 11: Givet en rekursiv algoritm: procedur F(n: heltal); börja om n > 1 börjar då F(n-2); F(n-1); F(n div 2); slutet; writeln("*"); slutet ; Hur många asterisker kommer att skrivas ut på skärmen när F(7) anropas? Svar: 88

Uppgift 12: Givet en rekursiv algoritm: procedur F(n: heltal); börja om n > 2 börjar sedan writeln("*"); F(n-2); F(n-1); F(n div 2); slutet ; writeln("*"); slutet; Hur många asterisker kommer att skrivas ut på skärmen när F(6) anropas? Svar: 33

Uppgift 13: Givet en rekursiv algoritm: procedur F (n: heltal); börja skrivaln(n); om n

Uppgift 14: Givet en rekursiv algoritm: procedur F (n: heltal); börja skrivaln(n); om n

Uppgift 15: Givet en rekursiv algoritm: procedur F (n: heltal); börja skrivaln(n); om n

Uppgift 16: Givet en rekursiv algoritm: procedur F (n: heltal); börja skrivaln(n); om n

Uppgift 17: Givet en rekursiv algoritm: procedur F (n: heltal); börja skrivaln(n); om n

Uppgift 18: Givet en rekursiv algoritm: procedur F (n: heltal); börja skrivaln(n); om n

Uppgift 19: Givet en rekursiv algoritm: procedur F (n: heltal); börja skrivaln(n); om n

Uppgift 20: Givet en rekursiv algoritm: procedur F (n: heltal); börja skrivaln(n); om n

Uppgift 21: Givet en rekursiv algoritm: procedur F (n: heltal); börja skrivaln(n); om n

Uppgift 22: Givet en rekursiv algoritm: procedur F (n: heltal); börja skrivaln(n); om n

Uppgift 23: Givet en rekursiv algoritm: procedur F (n: heltal); börja skrivaln(n); om n

Uppgift 24: Givet en rekursiv algoritm: procedur F (n: heltal); börja skrivaln(n); om n

Uppgift 25: Givet en rekursiv algoritm: procedur F (n: heltal); börja skrivaln(n); om n

Rekursion är när en subrutin anropar sig själv. När de står inför en sådan algoritmisk design för första gången upplever de flesta vissa svårigheter, men med lite övning kommer rekursion att bli ett förståeligt och mycket användbart verktyg i din programmeringsarsenal.

1. Kärnan i rekursion

En procedur eller funktion kan innehålla anrop till andra procedurer eller funktioner. Förfarandet kan också kalla sig. Det finns ingen paradox här - datorn exekverar endast sekventiellt de kommandon den stöter på i programmet och om den stöter på ett proceduranrop börjar den helt enkelt utföra denna procedur. Det spelar ingen roll vilken procedur som gav kommandot att göra detta.

Exempel på ett rekursivt förfarande:

Procedur Rec(a: heltal); börja om a>

Låt oss överväga vad som händer om ett anrop, till exempel av formen Rec(3) görs i huvudprogrammet. Nedan finns ett flödesschema som visar exekveringssekvensen för programsatserna.

Ris. 1. Blockschema över det rekursiva förfarandet.

Procedur Rec anropas med parameter a = 3. Den innehåller ett anrop till procedur Rec med parameter a = 2. Det föregående anropet har inte slutförts ännu, så du kan tänka dig att en annan procedur skapas och den första slutar inte sitt arbete förrän det slutar. Anropsprocessen avslutas när parameter a = 0. Vid denna tidpunkt exekveras 4 instanser av proceduren samtidigt. Antalet samtidigt utförda procedurer anropas rekursionsdjup.

Den fjärde proceduren som kallas (Rec(0)) kommer att skriva ut siffran 0 och avsluta sitt arbete. Efter detta återgår kontrollen till proceduren som anropade den (Rec(1)) och siffran 1 skrivs ut. Och så vidare tills alla procedurer är slutförda. Det ursprungliga samtalet kommer att skriva ut fyra nummer: 0, 1, 2, 3.

En annan visuell bild av vad som händer visas i fig. 2.

Ris. 2. Exekvera Rec-proceduren med parameter 3 består av att utföra Rec-proceduren med parameter 2 och skriva ut siffran 3. I sin tur består Rec-proceduren med parameter 2 av att utföra Rec-proceduren med parameter 1 och skriva ut siffran 2. Etc .

Som en övning på egen hand, överväg vad som händer när du ringer Rec(4). Tänk också på vad som skulle hända om du anropade Rec2(4)-proceduren nedan, med operatörerna omvända.

Procedur Rec2(a: heltal); börja skrivaln(a); om a>0 då Rec2(a-1); slutet;

Observera att i dessa exempel finns det rekursiva anropet i ett villkorligt uttalande. Detta är en nödvändig förutsättning för att rekursionen någonsin ska ta slut. Observera också att proceduren anropar sig själv med en annan parameter än den som den anropades med. Om proceduren inte använder globala variabler är detta också nödvändigt för att inte rekursionen ska fortsätta i det oändliga.

Ett lite mer komplext schema är möjligt: funktion A anropar funktion B, som i sin tur anropar A. Detta kallas komplex rekursion. Det visar sig att det förfarande som beskrivs först måste kalla ett förfarande som ännu inte har beskrivits. För att detta ska vara möjligt måste du använda .

Procedur A(n: heltal); (Vidarebeskrivning (rubrik) av den första proceduren) procedur B(n: heltal); (Beskrivning av den andra proceduren framåt) procedur A(n: heltal); (Fullständig beskrivning av procedur A) börja skrivaln(n); B(n-1); slutet; procedur B(n: heltal); (Fullständig beskrivning av procedur B) börja skrivaln(n); om n

Den framåtriktade deklarationen av procedur B gör att den kan anropas från procedur A. Den framåtriktade deklarationen av procedur A krävs inte i detta exempel och läggs till av estetiska skäl.

Om vanlig rekursion kan liknas vid en ouroboros (fig. 3), så kan bilden av komplex rekursion hämtas från den berömda barndikten, där "Vargarna blev rädda och åt upp varandra." Föreställ dig att två vargar äter upp varandra och du kommer att förstå komplex rekursion.

Ris. 3. Ouroboros - en orm som slukar sin egen svans. Ritning från den alkemiska avhandlingen "Synosius" av Theodore Pelecanos (1478).

Ris. 4. Komplex rekursion.

3. Simulera en loop med hjälp av rekursion

Om en procedur anropar sig själv, gör den i huvudsak att instruktionerna den innehåller exekveras igen, liknande en loop. Vissa programmeringsspråk innehåller inte looping-konstruktioner alls, vilket gör att programmerare kan organisera upprepningar med hjälp av rekursion (till exempel Prolog, där rekursion är en grundläggande programmeringsteknik).

Låt oss till exempel simulera driften av en for-loop. För att göra detta behöver vi en stegräknarevariabel, som till exempel kan implementeras som en procedurparameter.

Exempel 1.

Procedur LoopImitation(i, n: heltal); (Den första parametern är stegräknaren, den andra parametern är det totala antalet steg) begin writeln("Hej N", i); //Här är några instruktioner som kommer att upprepas om jag

Resultatet av ett anrop av formuläret LoopImitation(1, 10) kommer att vara exekvering av instruktioner tio gånger, vilket ändrar räknaren från 1 till 10. I det här fallet kommer följande att skrivas ut:

Hej N 1
Hej N 2
…
Hej N 10

I allmänhet är det inte svårt att se att parametrarna för proceduren är gränserna för att ändra räknarvärdena.

Du kan byta det rekursiva samtalet och instruktionerna som ska upprepas, som i följande exempel.

Exempel 2.

Procedur LoopImitation2(i, n: heltal); börja om jag

I detta fall kommer ett rekursivt proceduranrop att ske innan instruktioner börjar exekveras. Den nya instansen av proceduren kommer också, först och främst, att anropa en annan instans, och så vidare, tills vi når maxvärdet på räknaren. Först efter detta kommer den sista av de anropade procedurerna att utföra sina instruktioner, sedan kommer den näst sista att utföra sina instruktioner, etc. Resultatet av att anropa LoopImitation2(1, 10) blir att skriva ut hälsningar i omvänd ordning:

Hej N 10
…
Hej N 1

Om vi föreställer oss en kedja av rekursivt kallade procedurer, så går vi i exempel 1 igenom den från tidigare anropade procedurer till senare. I exempel 2, tvärtom, från senare till tidigare.

Slutligen kan ett rekursivt anrop placeras mellan två block av instruktioner. Till exempel:

Procedur LoopImitation3(i, n: heltal); begin writeln("Hej N", i); (Det första blocket med instruktioner kan finnas här) om jag

Här exekveras först instruktionerna från det första blocket sekventiellt, sedan exekveras instruktionerna från det andra blocket i omvänd ordning. När vi anropar LoopImitation3(1, 10) får vi:

Hej N 1
…
Hej N 10
Hej N 10
…
Hej N 1

Det skulle ta två slingor för att göra samma sak utan rekursion.

Du kan dra fördel av det faktum att utförandet av delar av samma procedur fördelas över tiden. Till exempel:

Exempel 3: Konvertera ett tal till binärt.

Att erhålla siffrorna i ett binärt tal, som bekant, sker genom att dividera med en rest med basen i talsystemet 2. Om det finns ett tal är dess sista siffra i dess binära representation lika med

Att ta hela delen av division med 2:

vi får ett tal som har samma binära representation, men utan sista siffran. Det räcker alltså att upprepa de två ovanstående operationerna tills nästa divisionsfält får en heltalsdel lika med 0. Utan rekursion kommer det att se ut så här:

Medan x>0 börjar c:=x mod 2; x:=x div 2; skriv(c); slutet;

Problemet här är att siffrorna i den binära representationen beräknas i omvänd ordning (senast först). För att skriva ut ett nummer i normal form måste du komma ihåg alla siffror i arrayelementen och skriva ut dem i en separat slinga.

Med hjälp av rekursion är det inte svårt att uppnå utdata i rätt ordning utan en array och en andra loop. Nämligen:

Procedur Binärrepresentation(x: heltal); var c, x: heltal; start (Första blocket. Utförs i ordning efter proceduranrop) c:= x mod 2; x:= x div 2; (Rekursivt anrop) om x>0 då BinaryRepresentation(x); (Andra blocket. Utförs i omvänd ordning) write(c); slutet;

Generellt sett fick vi inga vinster. Siffrorna i den binära representationen lagras i lokala variabler, som är olika för varje pågående instans av den rekursiva proceduren. Det vill säga att det inte gick att spara minne. Tvärtom slösar vi extra minne på att lagra många lokala variabler x. Den här lösningen verkar dock vacker för mig.

4. Återkommande relationer. Rekursion och iteration

En sekvens av vektorer sägs ges av en återkommande relation om den initiala vektorn och det funktionella beroendet av den efterföljande vektorn på den föregående ges

Ett enkelt exempel på en kvantitet som beräknas med hjälp av återfallsrelationer är faktorialen

Nästa faktor kan beräknas från den föregående som:

Genom att introducera notationen får vi relationen:

Vektorerna från formel (1) kan tolkas som uppsättningar av variabelvärden. Sedan kommer beräkningen av det nödvändiga elementet i sekvensen att bestå av upprepad uppdatering av deras värden. Särskilt för factorial:

X:= 1; för i:= 2 till n gör x:= x * i; skrivln(x);

Varje sådan uppdatering (x:= x * i) anropas iteration, och processen att upprepa iterationer är iteration.

Låt oss dock notera att relation (1) är en rent rekursiv definition av sekvensen och beräkningen av det n:te elementet är faktiskt den upprepade tagningen av funktionen f från sig själv:

Speciellt, för factorial kan man skriva:

Funktionsfaktor(n: heltal): heltal; börja om n > 1 då Faktoriell:= n * Faktoriell(n-1) annars Faktoriell:= 1; slutet;

Det bör förstås att anropsfunktioner medför ytterligare overhead, så det första alternativet för att beräkna faktorvärdet kommer att vara något snabbare. I allmänhet fungerar iterativa lösningar snabbare än rekursiva.

Innan vi går vidare till situationer där rekursion är användbar, låt oss titta på ytterligare ett exempel där det inte bör användas.

Låt oss överväga ett specialfall av återkommande relationer, när nästa värde i sekvensen inte beror på en, utan på flera tidigare värden samtidigt. Ett exempel är den berömda Fibonacci-sekvensen, där varje nästa element är summan av de två föregående:

Med ett "frontalt" tillvägagångssätt kan du skriva:

Funktion Fib(n: heltal): heltal; börja om n > 1 så Fib:= Fib(n-1) + Fib(n-2) annars Fib:= 1; slutet;

Varje Fib-samtal skapar två kopior av sig själv, varje kopia skapar två till, och så vidare. Antalet operationer ökar med antalet n exponentiellt, men med en iterativ lösning linjär in n antal operationer.

Faktum är att exemplet ovan lär oss inte NÄR rekursion bör inte användas, annars HUR den ska inte användas. När allt kommer omkring, om det finns en snabb iterativ (loopbaserad) lösning, kan samma loop implementeras med hjälp av en rekursiv procedur eller funktion. Till exempel:

// x1, x2 – initiala villkor (1, 1) // n – nummer för den obligatoriska Fibonacci-talfunktionen Fib(x1, x2, n: heltal): heltal; var x3: heltal; börja om n > 1 börjar sedan x3:= x2 + x1; xl:= x2; x2:= x3; Fib:= Fib(xl, x2, n-1); end else Fib:= x2; slutet;

Ändå är iterativa lösningar att föredra. Frågan är, när ska rekursion användas i detta fall?

Alla rekursiva procedurer och funktioner som bara innehåller ett rekursivt anrop till sig själva kan enkelt ersättas av iterativa loopar. För att få något som inte har en enkel icke-rekursiv motsvarighet måste du tillgripa procedurer och funktioner som kallar sig två eller flera gånger. I det här fallet bildar uppsättningen av anropade procedurer inte längre en kedja, som i fig. 1, men ett helt träd. Det finns breda klasser av problem när beräkningsprocessen måste organiseras på detta sätt. För dem kommer rekursion att vara den enklaste och mest naturliga lösningen.

5. Träd

Den teoretiska grunden för rekursiva funktioner som kallar sig mer än en gång är den gren av diskret matematik som studerar träd.

5.1. Grundläggande definitioner. Sätt att avbilda träd

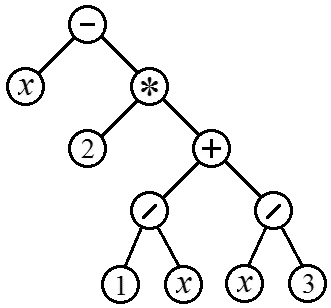
Definition: vi kommer att kalla den finita mängden T, bestående av en eller flera noder så att:
a) Det finns en speciell nod som kallas roten till detta träd.
b) De återstående noderna (exklusive roten) finns i parvis disjunkta delmängder, som var och en i sin tur är ett träd. Träd kallas underträd av detta träd.

Denna definition är rekursiv. Kort sagt är ett träd en uppsättning som består av en rot och underträd fästa vid den, som också är träd. Ett träd definieras genom sig självt. Men denna definition är vettig eftersom rekursion är ändlig. Varje underträd innehåller färre noder än dess innehållande träd. I slutändan kommer vi till underträd som bara innehåller en nod, och det är redan klart vad det är.

Ris. 3. Träd.

I fig. Figur 3 visar ett träd med sju noder. Även om vanliga träd växer från botten till toppen, är det vanligt att rita dem tvärtom. När du ritar ett diagram för hand är denna metod uppenbarligen mer bekväm. På grund av denna inkonsekvens uppstår ibland förvirring när en nod sägs vara över eller under en annan. Av denna anledning är det bekvämare att använda den terminologi som används när man beskriver släktträd, kallar noder närmare rotförfäderna och mer avlägsna ättlingar.

Ett träd kan avbildas grafiskt på andra sätt. Några av dem visas i fig. 4. Enligt definitionen är ett träd ett system av kapslade uppsättningar, där dessa uppsättningar antingen inte skär varandra eller är helt inneslutna i varandra. Sådana uppsättningar kan avbildas som regioner på ett plan (fig. 4a). I fig. 4b är de kapslade uppsättningarna inte placerade i ett plan, utan är förlängda till en linje. Ris. 4b kan också ses som ett diagram över någon algebraisk formel som innehåller kapslade parenteser. Ris. Figur 4c ger ett annat populärt sätt att representera en trädstruktur som en förskjuten lista.

Ris. 4. Andra sätt att avbilda trädstrukturer: (a) kapslade uppsättningar; (b) kapslade parenteser; c) Koncessionsförteckning.

Den förskjutna listan har uppenbara likheter med hur programkoden formateras. Ett program skrivet inom ramen för det strukturerade programmeringsparadigmet kan faktiskt representeras som ett träd som består av kapslade strukturer.

Du kan också dra en analogi mellan den stegvisa listan och utseendet på innehållsförteckningar i böcker, där avsnitt innehåller underavdelningar, som i sin tur innehåller underavdelningar osv. Det traditionella sättet att numrera sådana avsnitt (avsnitt 1, avsnitt 1.1 och 1.2, avsnitt 1.1.2 etc.) kallas Deweys decimalsystem. Applicerad på trädet i fig. 3 och 4 kommer detta system att ge:

1. A; 1.IB; 1,2 C; 1.2.1 D; 1.2.2 E; 1.2.3 F; 1.2.3.1 G;

5.2. Passerande träd

I alla algoritmer relaterade till trädstrukturer dyker alltid samma idé upp, nämligen idén godkänd eller trädpassering. Detta är ett sätt att besöka trädnoder där varje nod korsas exakt en gång. Detta resulterar i ett linjärt arrangemang av trädnoder. I synnerhet finns det tre sätt: du kan gå igenom noderna i framåt-, omvänd- och slutordning.

Framåtgående traversalalgoritm:

Gå till roten
Gå igenom alla underträd från vänster till höger i direkt ordning.

Denna algoritm är rekursiv, eftersom korsningen av ett träd innehåller korsningen av underträd, och de i sin tur korsas med samma algoritm.

I synnerhet för trädet i fig. 3 och 4 ger direkt genomgång en sekvens av noder: A, B, C, D, E, F, G.

Den resulterande sekvensen motsvarar en uppräkning av noder från vänster till höger när ett träd representeras med kapslade parenteser och i Dewey-decimalnotation, såväl som en passage uppifrån och ned när den representeras som en förskjuten lista.

När man implementerar denna algoritm i ett programmeringsspråk, motsvarar det att slå roten mot proceduren eller funktionen som utför vissa åtgärder, och att gå igenom underträd motsvarar rekursiva anrop till sig själv. Speciellt för ett binärt träd (där varje nod har högst två underträd), skulle motsvarande procedur se ut så här:

// Preorder Traversal – engelskt namn för direktbeställningsprocedur PreorderTraversal((Argument)); börja //Passar roten DoSomething((Argument)); //Övergång av det vänstra underträdet om (Det finns ett underträd till vänster) sedan PreorderTransversal((Argument 2)); //Övergång av höger underträd om (Det finns ett höger underträd) sedan PreorderTransversal((Argument 3)); slutet;

Det vill säga, först utför proceduren alla åtgärder, och först därefter inträffar alla rekursiva anrop.

Omvänd traversalalgoritm:

Gå igenom det vänstra underträdet,
Gå till roten
Gå igenom nästa underträd till vänster.
Gå till roten
etc. tills underträdet längst till höger korsas.

Det vill säga att alla underträd korsas från vänster till höger, och återgången till roten ligger mellan dessa traverseringar. För trädet i fig. 3 och 4 ger detta sekvensen av noder: B, A, D, C, E, G, F.

I en motsvarande rekursiv procedur kommer åtgärderna att placeras i mellanrummen mellan de rekursiva anropen. Specifikt för ett binärt träd:

// Inorder Traversal – engelskt namn för proceduren för omvänd ordning InorderTraversal((Argument)); börja //Resa det vänstra underträdet om (Ett vänster underträd finns) sedan InorderTraversal((Argument 2)); //Passar roten DoSomething((Argument)); //Traverse the right subtree if (Ett höger subtree exists) then InorderTraversal((Argument 3)); slutet;

End-order traversal algoritm:

Gå igenom alla underträd från vänster till höger,
Gå till roten.

För trädet i fig. 3 och 4 kommer detta att ge sekvensen av noder: B, D, E, G, F, C, A.

I en motsvarande rekursiv procedur kommer åtgärderna att lokaliseras efter de rekursiva anropen. Specifikt för ett binärt träd:

// Postorder Traversal – engelskt namn för slutorderproceduren PostorderTraversal((Argument)); begin //Resa i det vänstra underträdet if (Det finns ett underträd till vänster) sedan PostorderTraversal((Argument 2)); //Överskrider det högra underträdet om (Ett högerunderträd finns) sedan PostorderTraversal((Argument 3)); //Passar roten DoSomething((Argument)); slutet;

5.3. Representation av ett träd i datorns minne

Om viss information finns i trädnoder kan en lämplig dynamisk datastruktur användas för att lagra den. I Pascal görs detta med en posttypvariabel som innehåller pekare till underträd av samma typ. Till exempel kan ett binärt träd där varje nod innehåller ett heltal lagras med en variabel av typen PTree, som beskrivs nedan:

Skriv PTree = ^TTree; TTree = post Inf: heltal; LeftSubTree, RightSubTree: PTree; slutet;

Varje nod har en PTree-typ. Detta är en pekare, vilket betyder att varje nod måste skapas genom att anropa den nya proceduren på den. Om noden är en lövnod tilldelas dess LeftSubTree- och RightSubTree-fält värdet noll. Annars skapas LeftSubTree- och RightSubTree-noderna också av New-proceduren.

En sådan post visas schematiskt i fig. 5.

Ris. 5. Schematisk representation av en TTree-typpost. Posten har tre fält: Inf – ett nummer, LeftSubTree och RightSubTree – pekare till poster av samma TTree-typ.

Ett exempel på ett träd som består av sådana poster visas i figur 6.

Ris. 6. Ett träd som består av poster av typen TTree. Varje post lagrar ett nummer och två pekare som kan innehålla antingen noll, eller adresser till andra poster av samma typ.

Om du inte tidigare har arbetat med strukturer som består av poster innehållande länkar till poster av samma typ rekommenderar vi att du bekantar dig med materialet om.

6. Exempel på rekursiva algoritmer

6.1. Rita ett träd

Låt oss överväga algoritmen för att rita trädet som visas i fig. 6. Om varje linje anses vara en nod, så uppfyller denna bild helt definitionen av ett träd som gavs i föregående avsnitt.

Ris. 6. Träd.

Den rekursiva proceduren skulle uppenbarligen rita en linje (stammen upp till den första grenen), och sedan kalla sig för att rita de två underträden. Underträd skiljer sig från trädet som innehåller dem i koordinaterna för deras startpunkt, rotationsvinkel, stamlängd och antalet grenar de innehåller (en mindre). Alla dessa skillnader bör göras parametrar för den rekursiva proceduren.

Ett exempel på en sådan procedur, skriven i Delphi, presenteras nedan:

Procedur Träd(Canvas: TCanvas; //Duk som trädet kommer att ritas på x,y: utsträckt; //Rotkoordinater Vinkel: utsträckt; //Vinkel vid vilken trädet växer Stamlängd: utsträckt; //Stamlängd n: heltal / /Antal filialer (hur många fler //rekursiva samtal kvar)); var x2, y2: utökad; //Trunk slut (grenpunkt) börjar x2:= x + TrunkLength * cos(Angle); y2:= y - TrunkLength * sin(Angle); Canvas.MoveTo(runda(x), rund(y)); Canvas.LineTo(runda(x2), rund(y2)); om n > 1 börjar sedan Träd(Canvas, x2, y2, Angle+Pi/4, 0,55*TrunkLength, n-1); Träd(Canvas, x2, y2, Angle-Pi/4, 0,55*TrunkLength, n-1); slutet; slutet;

För att få Fig. 6 denna procedur anropades med följande parametrar:

Träd(Bild1. Canvas, 175, 325, Pi/2, 120, 15);

Observera att ritning utförs före rekursiva anrop, det vill säga att trädet ritas i direkt ordning.

6.2. Hanoi Towers

Enligt legenden i det stora templet i Banaras, under katedralen som markerar mitten av världen, finns en bronsskiva på vilken 3 diamantstavar är fixerade, en aln hög och tjock som ett bi. För länge sedan, i början av tiderna, begick munkarna i detta kloster anstöt inför guden Brahma. Rasande reste Brahma tre höga stavar och placerade 64 skivor av rent guld på en av dem, så att varje mindre skiva vilade på en större. Så snart alla 64 skivorna har överförts från staven som Gud Brahma placerade dem på när han skapade världen, till en annan stav, kommer tornet tillsammans med templet att förvandlas till damm och världen kommer att förgås under åskslag.
Processen kräver att den större disken aldrig hamnar ovanpå den mindre. Munkarna befinner sig i ett dilemma: i vilken ordning ska de göra växlingarna? Det krävs att de förses med programvara för att beräkna denna sekvens.

Oberoende av Brahma lades detta pussel i slutet av 1800-talet av den franske matematikern Edouard Lucas. Den sålda versionen använde vanligtvis 7-8 skivor (fig. 7).

Ris. 7. Pussel "Towers of Hanoi".

Låt oss anta att det finns en lösning för n-1 skiva. Sedan för att växla n diskar, fortsätt enligt följande:

1) Skift n-1 skiva.
2) Skift n disken på det återstående lediga stiftet.
3) Vi flyttar stacken från n-1 skiva mottagen i punkt (1) överst n-th disk.

För för fallet n= 1 omarrangeringsalgoritmen är uppenbar, sedan genom induktion, med hjälp av åtgärder (1) – (3), kan vi ordna om ett godtyckligt antal diskar.

Låt oss skapa en rekursiv procedur som skriver ut hela sekvensen av omarrangemang för ett givet antal diskar. Varje gång en sådan procedur anropas måste den skriva ut information om ett skift (från punkt 2 i algoritmen). För omarrangemang från punkterna (1) och (3) kommer proceduren att anropas med antalet diskar reducerat med en.

//n – antal diskar //a, b, c – pin-nummer. Växling görs från stift a, //till stift b med hjälpstift c. procedur Hanoi(n, a, b, c: heltal); börja om n > 1 börjar sedan Hanoi(n-1, a, c, b); writeln(a, " ->", b); Hanoi (n-1, c, b, a); end else writeln(a, " ->", b); slutet;

Observera att uppsättningen av rekursivt anropade procedurer i detta fall bildar ett träd som korsas i omvänd ordning.

6.3. Analysera aritmetiska uttryck

Uppgiften med att analysera är att beräkna värdet på uttrycket med hjälp av en befintlig sträng som innehåller ett aritmetiskt uttryck och de kända värdena för variablerna som ingår i det.

Processen att beräkna aritmetiska uttryck kan representeras som ett binärt träd. Faktum är att var och en av de aritmetiska operatorerna (+, –, *, /) kräver två operander, som också kommer att vara aritmetiska uttryck och följaktligen kan betraktas som underträd. Ris. Figur 8 visar ett exempel på ett träd som motsvarar uttrycket:

Ris. 8. Syntaxträd som motsvarar det aritmetiska uttrycket (6).

I ett sådant träd kommer slutnoderna alltid att vara variabler (här x) eller numeriska konstanter, och alla interna noder kommer att innehålla aritmetiska operatorer. För att köra en operator måste du först utvärdera dess operander. Således bör trädet i figuren korsas i terminal ordning. Motsvarande sekvens av noder

kallad omvänd polsk notation aritmetiskt uttryck.

När du konstruerar ett syntaxträd bör du vara uppmärksam på följande funktion. Om det till exempel finns ett uttryck

och vi kommer att läsa operationerna för addition och subtraktion från vänster till höger, då kommer det korrekta syntaxträdet att innehålla ett minus istället för ett plus (Fig. 9a). I grund och botten motsvarar detta träd uttrycket.Det är möjligt att göra skapandet av ett träd lättare om du analyserar uttryck (8) omvänt, från höger till vänster. I det här fallet är resultatet ett träd med Fig. 9b, motsvarande träd 8a, men kräver inte byte av skyltar.

På samma sätt, från höger till vänster, måste du analysera uttryck som innehåller multiplikations- och divisionsoperatorer.

Ris. 9. Syntaxträd för uttryck a – b + c när man läser från vänster till höger (a) och från höger till vänster (b).

Detta tillvägagångssätt eliminerar inte helt rekursion. Det låter dig dock begränsa dig till endast ett anrop till en rekursiv procedur, vilket kan vara tillräckligt om motivet är att maximera prestanda.

7.3. Bestämma en trädnod genom dess nummer

Tanken med detta tillvägagångssätt är att ersätta rekursiva anrop med en enkel loop som kommer att exekveras så många gånger som det finns noder i trädet som bildas av de rekursiva procedurerna. Exakt vad som kommer att göras vid varje steg bör bestämmas av stegnumret. Att jämföra stegnumret och de nödvändiga åtgärderna är inte en trivial uppgift och i varje fall måste det lösas separat.

Låt oss till exempel säga att du vill göra k kapslade slingor n steg i varje:

För i1:= 0 till n-1 gör för i2:= 0 till n-1 gör för i3:= 0 till n-1 gör …

Om kär okänt i förväg är det omöjligt att skriva dem explicit, som visas ovan. Med hjälp av tekniken som visas i avsnitt 6.5 kan du få det erforderliga antalet kapslade loopar med hjälp av en rekursiv procedur:

Procedur NestedCycles(Index: array av heltal; n, k, djup: heltal); var i: heltal; börja om djup

För att bli av med rekursion och reducera allt till en cykel, notera att om du numrerar stegen i radixtalsystemet n, då har varje steg ett nummer som består av siffrorna i1, i2, i3, ... eller motsvarande värden från indexmatrisen. Det vill säga siffrorna motsvarar värdena på cykelräknarna. Stegnummer i vanlig decimalnotation:

Det blir totalt steg n k. Genom att gå igenom deras tal i decimaltalssystemet och omvandla var och en av dem till radixsystemet n, får vi indexvärdena:

M:= round(IntPower(n, k)); för i:= 0 till M-1 börjar Number:= i; för p:= 0 till k-1 börjar Index:= Number mod n; Antal:= Antal div n; slutet; DoSomething(Index); slutet;

Låt oss återigen notera att metoden inte är universell och du måste komma på något annat för varje uppgift.

Kontrollfrågor

1. Bestäm vad följande rekursiva procedurer och funktioner kommer att göra.

(a) Vad kommer följande procedur att skrivas ut när Rec(4) anropas?

Procedur Rec(a: heltal); börja skrivaln(a); om a>0 så Rec(a-1); skrivln(a); slutet;

(b) Vad blir värdet av funktionen Nod(78, 26)?

Funktion Nod(a, b: heltal): heltal; börja om a > b då Nod:= Nod(a – b, b) annars om b > a then Nod:= Nod(a, b – a) annars Nod:= a; slutet;

Procedur A(n: heltal); procedur B(n: heltal); procedur A(n: heltal); börja skrivaln(n); B(n-1); slutet; procedur B(n: heltal); börja skrivaln(n); om n

(d) Vad kommer proceduren nedan att skrivas ut när du anropar BT(0, 1, 3)?

Procedur BT(x: reell; D, MaxD: heltal); börja om D = MaxD så skrivln(x) annars börjar BT(x – 1, D + 1, MaxD); BT(x + 1, D + 1, MaxD); slutet; slutet;

2. Ouroboros - en orm som slukar sin egen svans (fig. 14) när den är utfälld har en längd L, diameter runt huvudet D, bukväggtjocklek d. Bestäm hur mycket svans han kan pressa in i sig själv och hur många lager kommer svansen att läggas i efter det?

Ris. 14. Expanderad ouroboros.

3. För trädet i fig. 10a indikerar sekvensen av besöksnoder i framåt-, bakåt- och änd-genomgångsordning.

4. Avbilda grafiskt trädet definierat med kapslade parenteser: (A(B(C, D), E), F, G).

5. Avbilda syntaxträdet grafiskt för följande aritmetiska uttryck:

Skriv detta uttryck i omvänd polsk notation.

6. För grafen nedan (fig. 15), skriv ner närliggande matris och incidensmatris.

Uppgifter

1. Efter att ha beräknat faktorn ett tillräckligt stort antal gånger (en miljon eller mer), jämför effektiviteten hos de rekursiva och iterativa algoritmerna. Hur mycket kommer exekveringstiden att skilja sig åt och hur kommer detta förhållande att bero på antalet vars factorial beräknas?

2. Skriv en rekursiv funktion som kontrollerar om parenteser är korrekt placerade i en sträng. Om arrangemanget är korrekt är följande villkor uppfyllda:

(a) antalet öppnande och avslutande parenteser är lika.
(b) inom vilket par som helst finns en öppning - motsvarande stängningsfäste, fästena är korrekt placerade.

Exempel på felaktig placering:)(, ())(, ())((), etc.

3. Linjen kan innehålla både runda och fyrkantiga parenteser. Varje öppningsfäste har ett motsvarande stängningsfäste av samma typ (rund - rund, fyrkantig - fyrkantig). Skriv en rekursiv funktion som kontrollerar om parenteserna är rätt placerade i detta fall.

Exempel på felaktig placering: ([)].

4. Antalet vanliga konsolstrukturer med längd 6 är 5: ()()(), (())(), ()(()), ((())), (()()).
Skriv ett rekursivt program för att generera alla vanliga parentesstrukturer med längd 2 n.

Notera: Korrekt parentesstruktur med minsta längd "()". Strukturer med längre längd erhålls från strukturer med kortare längd på två sätt:

a) om den mindre strukturen tas inom parentes,
(b) om två mindre strukturer skrivs i följd.

5. Skapa en procedur som skriver ut alla möjliga permutationer för heltal från 1 till N.

6. Skapa en procedur som skriver ut alla delmängder av uppsättningen (1, 2, ..., N).

7. Skapa en procedur som skriver ut alla möjliga representationer av det naturliga talet N som summan av andra naturliga tal.

8. Skapa en funktion som beräknar summan av arrayelementen med hjälp av följande algoritm: arrayen delas i hälften, summan av elementen i varje halva beräknas och adderas. Summan av elementen i halva arrayen beräknas med samma algoritm, det vill säga igen genom att dela på hälften. Divisioner sker tills de resulterande delarna av arrayen innehåller ett element vardera och att beräkna summan blir därför trivial.

Kommentar: Denna algoritm är ett alternativ. När det gäller arrayer med verkligt värde tillåter det vanligtvis mindre avrundningsfel.

10. Skapa en procedur som ritar Koch-kurvan (Figur 12).

11. Reproducera figuren. 16. I figuren, vid varje nästa iteration, är cirkeln 2,5 gånger mindre (denna koefficient kan göras till en parameter).

Litteratur

1. D. Knuth. Konsten att programmera datorer. v. 1. (avsnitt 2.3. "Träd").
2. N. Wirth. Algoritmer och datastrukturer.