Duotos dvi rekursinės funkcijos f ir g. Rekursiniai ir rekursiniai algoritmai. Pagrindiniai apibrėžimai. Medžių vaizdavimo būdai

Sukurtas pristatymas tema „Rekursiniai algoritmai“, skirtas parengti mokinius vieningam valstybiniam informatikos ir IKT egzaminui. Darbe nagrinėjamas rekursijos apibrėžimas ir pateikiami rekursyviai apibrėžtų grafinių objektų pavyzdžiai. Pristatyme pateikiami Vieningo valstybinio egzamino – 2015 informatikos demonstracinės versijos projekto Nr.11 užduoties sprendimo metodai. Pirmasis metodas apima skambučių medžio kūrimą, antrasis metodas išsprendžia problemą naudojant pakeitimo metodą. Nagrinėjami 4 užduočių sprendimo abiem būdais pavyzdžiai. Šiame pristatyme yra 25 pratimai treniruotėms su atsakymais iš Konstantino Polyakovo svetainės.

Parsisiųsti:

Peržiūra:

Norėdami naudoti pristatymo peržiūras, susikurkite „Google“ paskyrą ir prisijunkite prie jos: https://accounts.google.com

Skaidrių antraštės:

Užduotis Nr. 11 Vieningas valstybinis egzaminas (bazinis lygis, laikas - 5 min.) Rekursiniai algoritmai. Autorius – Savivaldybės švietimo įstaigos „71 vidurinė mokykla“ informatikos mokytojas Korotūnas O.V.

Ką reikia žinoti: Rekursija yra objekto ar proceso apibrėžimas, aprašymas, vaizdavimas šiame objekte arba pačiame procese, ty situacija, kai objektas yra savęs dalis. Rusijos Federacijos herbas – rekursyviai apibrėžtas grafinis objektas: jame pavaizduoto dvigalvio erelio dešinėje letenoje įsegtas skeptras, kurį vainikuoja mažesnė herbo kopija. Kadangi ant šio herbo dešinėje erelio letenoje yra ir skeptras, gaunama begalinė rekursija. Rekursyvus Rusijos herbas

Programuojant rekursija yra funkcijos iškvietimas iš savęs, tiesiogiai arba per kitas funkcijas, pavyzdžiui, funkcija A iškviečia funkciją B, o funkcija B – funkciją A. Įdėtų funkcijos arba procedūros iškvietimų skaičius vadinamas rekursijos gyliu. rekursijos pavyzdys: jei ant suknelės yra riebalų dėmių, nesijaudinkite. Alyvos dėmės pašalinamos su šarmo tirpalu.

Užduoties pavyzdys: Duotas rekursinis algoritmas: procedūra F(n: integer); pradėti writeln(n); jei n

Užduoties pavyzdys: Duotas rekursinis algoritmas: procedūra F(n: integer); pradėti rašyti (n) ; jei n

Užduoties pavyzdys: Duotas rekursinis algoritmas: procedūra F(n: integer); pradėti writeln(n); jei n 9 skaidrė

Užduoties pavyzdys: Duotas rekursinis algoritmas: procedūra F(n: integer); pradėti writeln(n); jei n 10 skaidrė

Užduoties pavyzdys: Duotas rekursinis algoritmas: procedūra F(n: integer); pradėti writeln(n); jei n 11 skaidrė

15 Pavyzdys Nr. 2: Duotas rekursinis algoritmas: procedūra F(n: sveikasis skaičius); pradėti writeln(n); jei n

Pavyzdys Nr. 2: Duotas rekursinis algoritmas: procedūra F(n: integer); pradėti writeln(n); jei n 13 skaidrė

Pavyzdys Nr. 3: Duotas rekursinis algoritmas: procedūra F(n: integer); pradėti writeln("*"); jei n > 0, tada prasideda F(n-2); F(n div 2) galas galas ; Kiek žvaigždučių bus atspausdinta ekrane skambinant F(7)? * Suskaičiavę „žvaigždučių“ skaičių, gauname 21 Šiame pavyzdyje ekrane rodomos ne parametro n reikšmės, o simbolis * * * * * * * * * * * * * * * * * * * * * *

Pavyzdys Nr. 3: Duotas rekursinis algoritmas: procedūra F(n: integer); pradėti writeln("*"); jei n > 0, tada prasideda F(n-2); F(n div 2) galas galas ; Kiek žvaigždučių bus atspausdinta ekrane skambinant F(7)? Išspręskime problemą be medžio. Tegul S(n) yra „žvaigždžių“, kurios bus išspausdintos skambinant F(n), skaičius. Tada 1+S(n-2)+ S(n div 2), n>0 1 , n Turime žinoti S(7). S(7)= 1 +S(5)+ S(3) S(5)= 1 +S(3)+S(2) S(3)= 1 +S(1)+S(1) S( 2)=1+S(0)+S(1)=1+1+S(1)=2+S(1) S(1)= 1+ S(-1)+S(0)=1+ 1+1=3 Atvirkščiai: S(2)=2+3=5 S(3)=1+3+3=7 S(5)=1+7+5=13 S(7)=1+ 13+ 7 = 21 S(n) =

Pavyzdys Nr. 4: procedūra F(n: sveikasis skaičius); pradėti, jei n 18 skaidrė

Pavyzdys Nr. 4: procedūra F(n: sveikasis skaičius); pradėti, jei n 19 skaidrė

Pavyzdys Nr. 4: procedūra F(n: sveikasis skaičius); pradėti, jei n

Treniruočių užduotys

1 uždavinys: Duotas rekursinis algoritmas: procedūra F(n: sveikasis skaičius); pradėti writeln("*"); jei n > 0, tada prasideda F(n-2); F(n div 2); F(n div 2); pabaiga pabaiga ; Kiek žvaigždučių bus atspausdinta ekrane skambinant F(5)? Atsakymas: 34

2 uždavinys: Duotas rekursinis algoritmas: procedūra F(n: sveikasis skaičius); pradėti writeln("*"); jei n > 0, tada prasideda F(n-2); F(n-2); F(n div 2); pabaiga pabaiga ; Kiek žvaigždučių bus atspausdinta ekrane skambinant F(6)? Atsakymas: 58

3 uždavinys: Duotas rekursinis algoritmas: procedūra F(n: sveikasis skaičius); pradėti writeln("*"); jei n > 0, tada prasideda F(n-3); F(n div 2); pabaiga pabaiga ; Kiek žvaigždučių bus atspausdinta ekrane skambinant F(7)? Atsakymas: 15

4 uždavinys: Duotas rekursinis algoritmas: procedūra F(n: sveikasis skaičius); pradėti writeln("*"); jei n > 0, tada prasideda F(n-3); F(n-2); F(n div 2); pabaiga pabaiga ; Kiek žvaigždučių bus atspausdinta ekrane skambinant F(7)? Atsakymas: 55

5 uždavinys: Duotas rekursinis algoritmas: procedūra F(n: sveikasis skaičius); pradėti writeln("*"); jei n > 0, tada prasideda F(n-3); F(n-2); F(n div 2); F(n div 2); pabaiga pabaiga ; Kiek žvaigždučių bus atspausdinta ekrane skambinant F(6)? Atsakymas: 97

6 uždavinys: Duotas rekursinis algoritmas: procedūra F(n: sveikasis skaičius); pradėti writeln("*"); jei n > 0, tada pradėkite writeln("*"); F(n-2); F(n div 2); pabaiga pabaiga ; Kiek žvaigždučių bus atspausdinta ekrane skambinant F(7)? Atsakymas: 31

7 uždavinys: Duotas rekursinis algoritmas: procedūra F(n: sveikasis skaičius); pradėti writeln("*"); jei n > 0, tada pradėkite writeln("*"); F(n-2); F(n div 2); F(n div 2); pabaigos galas; Kiek žvaigždučių bus atspausdinta ekrane skambinant F(7)? Atsakymas: 81

8 uždavinys: Duotas rekursinis algoritmas: procedūra F(n: sveikasis skaičius); pradėti writeln("*"); jei n > 0, tada pradėkite writeln("*"); F(n-2); F(n-2); F(n div 2); pabaigos galas; Kiek žvaigždučių bus atspausdinta ekrane skambinant F(6)? Atsakymas: 77

9 uždavinys: Duotas rekursinis algoritmas: procedūra F(n: sveikasis skaičius); pradėti, jei n > 0, tada pradėti F(n-2); F(n-1); F(n-1); galas; writeln("*"); galas ; Kiek žvaigždučių bus atspausdinta ekrane skambinant F(5)? Atsakymas: 148

10 uždavinys: Duotas rekursinis algoritmas: procedūra F(n: sveikasis skaičius); pradėti, jei n > 0, tada pradėti writeln("*"); F(n-2); F(n-1); F(n-1); galas; writeln("*"); galas; Kiek žvaigždučių bus atspausdinta ekrane skambinant F(5)? Atsakymas: 197

11 uždavinys: Duotas rekursinis algoritmas: procedūra F(n: sveikasis skaičius); pradėti, jei n > 1, tada pradėti F(n-2); F(n-1); F(n div 2); galas; writeln("*"); galas ; Kiek žvaigždučių bus atspausdinta ekrane skambinant F(7)? Atsakymas: 88

12 uždavinys: Duotas rekursinis algoritmas: procedūra F(n: sveikasis skaičius); pradėti, jei n > 2, tada pradėti writeln("*"); F(n-2); F(n-1); F(n div 2); galas ; writeln("*"); galas; Kiek žvaigždučių bus atspausdinta ekrane skambinant F(6)? Atsakymas: 33

13 uždavinys: Duotas rekursinis algoritmas: procedūra F (n: sveikasis skaičius); pradėti writeln(n); jei n

14 uždavinys: Duotas rekursinis algoritmas: procedūra F (n: sveikasis skaičius); pradėti writeln(n); jei n

15 uždavinys: Duotas rekursinis algoritmas: procedūra F (n: sveikasis skaičius); pradėti writeln(n); jei n

16 uždavinys: Duotas rekursinis algoritmas: procedūra F (n: sveikasis skaičius); pradėti writeln(n); jei n

17 uždavinys: Duotas rekursinis algoritmas: procedūra F (n: sveikasis skaičius); pradėti writeln(n); jei n

18 uždavinys: Duotas rekursinis algoritmas: procedūra F (n: sveikasis skaičius); pradėti writeln(n); jei n

19 uždavinys: Duotas rekursinis algoritmas: procedūra F (n: sveikasis skaičius); pradėti writeln(n); jei n

20 uždavinys: Duotas rekursinis algoritmas: procedūra F (n: sveikasis skaičius); pradėti writeln(n); jei n

21 uždavinys: Duotas rekursinis algoritmas: procedūra F (n: sveikasis skaičius); pradėti writeln(n); jei n

22 uždavinys: Duotas rekursinis algoritmas: procedūra F (n: sveikasis skaičius); pradėti writeln(n); jei n

23 uždavinys: Duotas rekursinis algoritmas: procedūra F (n: sveikasis skaičius); pradėti writeln(n); jei n

24 uždavinys: Duotas rekursinis algoritmas: procedūra F (n: sveikasis skaičius); pradėti writeln(n); jei n

25 uždavinys: Duotas rekursinis algoritmas: procedūra F (n: sveikasis skaičius); pradėti writeln(n); jei n

Rekursija yra tada, kai paprogramė iškviečia save. Pirmą kartą susidūrę su tokiu algoritminiu dizainu dauguma žmonių patiria tam tikrų sunkumų, tačiau šiek tiek pasipraktikavus rekursija taps suprantama ir labai naudinga priemone jūsų programavimo arsenale.

1. Rekursijos esmė

Procedūroje arba funkcijoje gali būti kitų procedūrų ar funkcijų iškvietimų. Procedūra taip pat gali vadintis pati. Čia nėra jokio paradokso – kompiuteris tik nuosekliai vykdo tas komandas, su kuriomis susiduria programoje, ir, susidūręs su procedūros iškvietimu, tiesiog pradeda vykdyti šią procedūrą. Nesvarbu, kokia procedūra davė komandą tai padaryti.

Rekursinės procedūros pavyzdys:

Procedūra Rec(a: sveikasis skaičius); pradėti, jei a>

Panagrinėkime, kas atsitiks, jei pagrindinėje programoje iškviečiamas, pavyzdžiui, Rec(3) formos. Žemiau yra struktūrinė schema, rodanti teiginių vykdymo seką.

Ryžiai. 1. Rekursinės procedūros blokinė schema.

Procedūra Rec iškviečiama parametru a = 3. Jame yra iškvietimas į procedūrą Rec su parametru a = 2. Ankstesnis iškvietimas dar nebaigtas, todėl galite įsivaizduoti, kad sukuriama kita procedūra ir pirmoji nebaigia savo darbo, kol tai baigiasi. Iškvietimo procesas baigiasi, kai parametras a = 0. Šiuo metu vienu metu vykdomi 4 procedūros atvejai. Vadinamas vienu metu atliekamų procedūrų skaičius rekursijos gylis.

Ketvirta procedūra, pavadinta (Rec(0)), išspausdins skaičių 0 ir baigs darbą. Po to valdiklis grįžta į procedūrą, kuri ją iškvietė (Rec(1)) ir spausdinamas skaičius 1 Ir taip toliau, kol bus baigtos visos procedūros. Pradiniame skambutyje bus išspausdinti keturi skaičiai: 0, 1, 2, 3.

Kitas vaizdinis to, kas vyksta, vaizdas parodytas fig. 2.

Ryžiai. 2. Rec procedūros vykdymas su 3 parametru susideda iš Rec procedūros vykdymo su 2 parametru ir numerio 3 išspausdinimo. Savo ruožtu Rec procedūros su 2 parametru vykdymas susideda iš Rec procedūros vykdymo su 1 parametru ir skaičiaus 2 atspausdinimo. .

Kaip savarankišką pratimą apsvarstykite, kas atsitiks, kai skambinate Rec(4). Taip pat pagalvokite, kas atsitiktų, jei toliau pateiktą Rec2(4) procedūrą, o operatoriai būtų pakeisti atvirkščiai.

Procedūra Rec2(a: sveikasis skaičius); pradėti writeln(a); jei a>0, tai Rec2(a-1); galas;

Atkreipkite dėmesį, kad šiuose pavyzdžiuose rekursinis skambutis yra sąlyginiame sakinyje. Tai būtina sąlyga, kad rekursija kada nors pasibaigtų. Taip pat atkreipkite dėmesį, kad procedūra išsikviečia save naudojant skirtingą parametrą nei tas, kuriuo ji buvo iškviesta. Jei procedūra nenaudoja visuotinių kintamųjų, tai taip pat būtina, kad rekursija nesitęstų neribotą laiką.

Galima šiek tiek sudėtingesnė schema: funkcija A iškviečia funkciją B, kuri savo ruožtu iškviečia A. Tai vadinama kompleksinė rekursija. Pasirodo, pirmiausia aprašyta procedūra turi iškviesti procedūrą, kuri dar nebuvo aprašyta. Kad tai būtų įmanoma, turite naudoti .

Procedūra A(n: sveikas skaičius); (Pirmosios procedūros aprašymas (antraštė)) procedūra B(n: sveikasis skaičius); (Antros procedūros aprašymas pirmyn) procedūra A(n: sveikasis skaičius); (Visas A procedūros aprašymas) begin writeln(n); B(n-1); galas; procedūra B(n: sveikas skaičius); (Visas B procedūros aprašymas) begin writeln(n); jei n

Išankstinė procedūros B deklaracija leidžia ją iškviesti iš procedūros A. Procedūros A išankstinė deklaracija šiame pavyzdyje nereikalinga ir pridedama dėl estetinių priežasčių.

Jei įprastą rekursiją galima palyginti su mūsųoboru (3 pav.), tai sudėtingos rekursijos vaizdą galima nubrėžti iš garsiosios vaikiškos poemos, kur „Vilkai išsigando ir valgė vienas kitą“. Įsivaizduokite, kaip du vilkai valgo vienas kitą, ir jūs suprasite sudėtingą rekursiją.

Ryžiai. 3. Ouroboros – gyvatė, ryjanti savo uodegą. Piešinys iš Theodore'o Pelecanoso alcheminio traktato „Synosius“ (1478).

Ryžiai. 4. Kompleksinė rekursija.

3. Ciklo modeliavimas naudojant rekursiją

Jei procedūra iškviečia save, iš esmės vėl įvykdomos joje esančios instrukcijos, panašiai kaip ciklas. Kai kuriose programavimo kalbose visiškai nėra kilpinių konstrukcijų, todėl programuotojai gali organizuoti pakartojimus naudodami rekursiją (pavyzdžiui, „Prolog“, kur rekursija yra pagrindinė programavimo technika).

Pavyzdžiui, imituokime a for ciklo veikimą. Norėdami tai padaryti, mums reikia žingsnių skaitiklio kintamojo, kuris gali būti įgyvendintas, pavyzdžiui, kaip procedūros parametras.

1 pavyzdys.

Procedūra LoopImitation(i, n: sveikasis skaičius); (Pirmasis parametras yra žingsnių skaitiklis, antrasis parametras yra bendras žingsnių skaičius) begin writeln("Labas N ", i); //Štai visos instrukcijos, kurios bus kartojamos, jei i

Formos LoopImitation(1, 10) iškvietimo rezultatas bus komandų vykdymas dešimt kartų, keičiant skaitiklį nuo 1 iki 10. Tokiu atveju bus atspausdinta:

Sveiki N1
Sveiki N2
…
Sveiki, N10

Apskritai nesunku pastebėti, kad procedūros parametrai yra ribos keičiant skaitiklio reikšmes.

Galite sukeisti rekursyvų skambutį ir instrukcijas, kurios bus kartojamos, kaip parodyta kitame pavyzdyje.

2 pavyzdys.

Procedūra LoopImitation2(i, n: sveikasis skaičius); pradėti, jei aš

Tokiu atveju, prieš pradedant vykdyti komandas, įvyks rekursinis procedūros iškvietimas. Naujasis procedūros egzempliorius taip pat pirmiausia iškvies kitą egzempliorių ir taip toliau, kol pasieksime maksimalią skaitiklio reikšmę. Tik po to paskutinė iš iškviestų procedūrų įvykdys savo instrukcijas, o po paskutinė – vykdys savo instrukcijas ir pan. Iškvietus LoopImitation2(1, 10), sveikinimai bus atspausdinti atvirkštine tvarka:

Sveiki, N10
…
Sveiki N1

Jei įsivaizduosime rekursyviai vadinamų procedūrų grandinę, tai 1 pavyzdyje pereiname nuo anksčiau vadintų procedūrų iki vėlesnių. 2 pavyzdyje, priešingai, nuo vėlesnio iki ankstesnio.

Galiausiai tarp dviejų instrukcijų blokų galima įdėti rekursinį skambutį. Pavyzdžiui:

Procedūra LoopImitation3(i, n: sveikasis skaičius); begin writeln("Labas N ", i); (Čia gali būti pirmasis instrukcijų blokas), jei i

Čia pirmojo bloko instrukcijos pirmiausia vykdomos nuosekliai, o po to antrojo bloko instrukcijos vykdomos atvirkštine tvarka. Skambindami LoopImitation3(1, 10) gauname:

Sveiki N1
…
Sveiki, N10
Sveiki, N10
…
Sveiki N1

Norint atlikti tą patį veiksmą be rekursijos, prireiktų dviejų kilpų.

Galite pasinaudoti tuo, kad tos pačios procedūros dalių vykdymas laikui bėgant yra paskirstytas. Pavyzdžiui:

3 pavyzdys: skaičiaus konvertavimas į dvejetainį.

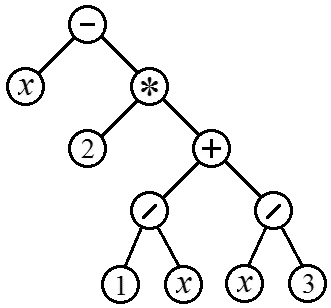
Dvejetainio skaičiaus skaitmenys, kaip žinoma, gaunami dalijant su likutimi iš skaičių sistemos 2 pagrindo. Jei yra skaičius, tada paskutinis jo skaitmuo dvejetainiame vaizde yra lygus

Paimant visą padalijimo iš 2 dalį:

gauname skaičių, kuris turi tą patį dvejetainį vaizdą, bet be paskutinio skaitmens. Taigi, pakanka kartoti pirmiau minėtas dvi operacijas, kol sekantis dalybos laukas gaus sveikąją dalį, lygią 0. Be rekursijos jis atrodys taip:

Nors x>0 pradėkite c:=x mod 2; x:=x div 2; rašyti (c); galas;

Problema ta, kad dvejetainio atvaizdo skaitmenys apskaičiuojami atvirkštine tvarka (naujausia pirmiausia). Norėdami atspausdinti skaičių įprasta forma, turėsite atsiminti visus masyvo elementų skaičius ir atspausdinti juos atskira kilpa.

Naudojant rekursiją, nesunku pasiekti išvestį teisinga tvarka be masyvo ir antros kilpos. Būtent:

Procedūra BinaryRepresentation(x: sveikasis skaičius); var c, x: sveikasis skaičius; begin (Pirmasis blokas. Vykdoma procedūrų iškvietimų tvarka) c:= x mod 2; x:= x div 2; (Rekursyvus skambutis) jei x>0, tada dvejetainis vaizdas(x); (Antras blokas. Vykdoma atvirkštine tvarka) write(c); galas;

Paprastai kalbant, jokių laimėjimų negavome. Dvejetainės reprezentacijos skaitmenys saugomi vietiniuose kintamuosiuose, kurie skiriasi kiekvienam vykdomam rekursinės procedūros egzemplioriui. Tai yra, nebuvo įmanoma išsaugoti atminties. Priešingai, eikvojame papildomą atmintį saugodami daug vietinių kintamųjų x. Tačiau šis sprendimas man atrodo gražus.

4. Pasikartojimo ryšiai. Rekursija ir iteracija

Sakoma, kad vektorių seka duota pasikartojimo ryšiu, jei pateikiamas pradinis vektorius ir paskesnio vektoriaus funkcinė priklausomybė nuo ankstesnio.

Paprastas dydžio, apskaičiuoto naudojant pasikartojimo ryšius, pavyzdys yra faktorialas

Kitas faktorialas gali būti apskaičiuotas pagal ankstesnį:

Įvesdami žymėjimą gauname ryšį:

(1) formulės vektoriai gali būti interpretuojami kaip kintamųjų reikšmių rinkiniai. Tada reikiamo sekos elemento apskaičiavimas susideda iš pakartotinio jų reikšmių atnaujinimo. Visų pirma faktorialams:

X: = 1; i:= 2 iki n daryti x:= x * i; writeln(x);

Kiekvienas toks atnaujinimas (x:= x * i) iškviečiamas iteracija, o iteracijų kartojimo procesas yra iteracija.

Tačiau atkreipkime dėmesį, kad santykis (1) yra grynai rekursinis sekos apibrėžimas, o n-ojo elemento apskaičiavimas iš tikrųjų yra pakartotinis funkcijos f paėmimas iš savęs:

Visų pirma, dėl faktorialo galima rašyti:

Funkcija Factorial(n: integer): sveikasis skaičius; pradėti, jei n > 1, tada faktorialus:= n * Faktorinis(n-1) else Faktorius:= 1; galas;

Reikėtų suprasti, kad funkcijų iškvietimas reikalauja tam tikrų papildomų išlaidų, todėl pirmoji faktorialo skaičiavimo parinktis bus šiek tiek greitesnė. Apskritai iteraciniai sprendimai veikia greičiau nei rekursyvūs.

Prieš pereidami prie situacijų, kai rekursija yra naudinga, pažvelkime į dar vieną pavyzdį, kur jos nereikėtų naudoti.

Panagrinėkime ypatingą pasikartojančių santykių atvejį, kai sekanti reikšmė iš eilės priklauso ne nuo vienos, o nuo kelių ankstesnių reikšmių vienu metu. Pavyzdys yra garsioji Fibonačio seka, kurioje kiekvienas kitas elementas yra dviejų ankstesnių elementų suma:

Naudodami „frontalinį“ metodą galite rašyti:

Funkcija Fib(n: integer): sveikasis skaičius; pradėti, jei n > 1, tada Fib:= Fib(n-1) + Fib(n-2) else Fib:= 1; galas;

Kiekvienas Fib skambutis sukuria dvi savo kopijas, kiekviena kopija sukuria dar dvi ir pan. Operacijų skaičius didėja kartu su skaičiumi n eksponentiškai, nors iteraciniam sprendimui tiesinis in n operacijų skaičius.

Tiesą sakant, aukščiau pateiktas pavyzdys to nemoko KADA Priešingu atveju rekursija neturėtų būti naudojama KAIP jis neturėtų būti naudojamas. Juk jei yra greitas iteracinis (ciklu pagrįstas) sprendimas, tai tą pačią kilpą galima įgyvendinti naudojant rekursinę procedūrą ar funkciją. Pavyzdžiui:

// x1, x2 – pradinės sąlygos (1, 1) // n – reikiamos Fibonačio skaičiaus funkcijos skaičius Fib(x1, x2, n: integer): sveikasis skaičius; var x3: sveikasis skaičius; pradėti, jei n > 1, tada pradėti x3:= x2 + x1; x1:= x2; x2:= x3; Fib:= Fib(x1, x2, n-1); pabaiga kita Fib:= x2; galas;

Vis dėlto pirmenybė teikiama iteraciniams sprendimams. Kyla klausimas, kada šiuo atveju reikėtų naudoti rekursiją?

Visos rekursinės procedūros ir funkcijos, kuriose yra tik vienas rekursinis skambutis į save, gali būti lengvai pakeistos kartotinėmis kilpomis. Norėdami gauti kažką, kas neturi paprasto nerekursyvaus atitikmens, turite pasinaudoti procedūromis ir funkcijomis, kurios vadinasi du ar daugiau kartų. Tokiu atveju iškviestų procedūrų rinkinys nebesudaro grandinės, kaip parodyta Fig. 1, bet visas medis. Yra daug problemų, kai skaičiavimo procesas turi būti organizuojamas tokiu būdu. Jiems rekursija bus paprasčiausias ir natūraliausias sprendimas.

5. Medžiai

Teorinis pagrindas rekursinėms funkcijoms, kurios save vadina ne kartą, yra diskrečiosios matematikos šaka, tirianti medžius.

5.1. Pagrindiniai apibrėžimai. Medžių vaizdavimo būdai

Apibrėžimas: vadinsime baigtinę aibę T, sudarytas iš vieno ar daugiau mazgų, kad:
a) Yra vienas specialus mazgas, vadinamas šio medžio šaknimi.
b) Likę mazgai (išskyrus šaknį) yra poromis nesujungtuose pogrupiuose, kurių kiekvienas savo ruožtu yra medis. Medžiai vadinami pomedžiaišio medžio.

Šis apibrėžimas yra rekursyvus. Trumpai tariant, medis yra rinkinys, susidedantis iš šaknies ir prie jos pritvirtintų pomedžių, kurie taip pat yra medžiai. Medis apibrėžiamas per save. Tačiau šis apibrėžimas yra prasmingas, nes rekursija yra baigtinė. Kiekviename pomedyje yra mažiau mazgų nei medyje, kuriame jis yra. Galų gale mes pasiekiame pomedžius, kuriuose yra tik vienas mazgas, ir tai jau aišku, kas tai yra.

Ryžiai. 3. Medis.

Fig. 3 paveiksle pavaizduotas medis su septyniais mazgais. Nors paprasti medžiai auga iš apačios į viršų, įprasta juos piešti atvirkščiai. Braižant schemą ranka, šis metodas akivaizdžiai patogesnis. Dėl šio nenuoseklumo kartais kyla painiavos, kai sakoma, kad vienas mazgas yra aukščiau arba žemiau kito. Dėl šios priežasties patogiau vartoti terminus, vartojamus apibūdinant giminės medžius, vadinant arčiau šaknų esančius protėvius, o toliau esančius palikuonimis.

Grafiškai medis gali būti pavaizduotas kitais būdais. Kai kurie iš jų parodyti fig. 4. Pagal apibrėžimą medis yra įdėtųjų aibių sistema, kai šios aibės arba nesikerta, arba yra visiškai viena kitoje. Tokius rinkinius galima pavaizduoti kaip sritis plokštumoje (4a pav.). Fig. 4b, įdėtos rinkiniai nėra plokštumoje, o yra pailgi į vieną liniją. Ryžiai. 4b taip pat galima žiūrėti kaip kai kurios algebrinės formulės diagramą su įdėtais skliaustais. Ryžiai. 4c paveiksle pateikiamas kitas populiarus būdas pavaizduoti medžio struktūrą kaip laipsnišką sąrašą.

Ryžiai. 4. Kiti medžio struktūrų vaizdavimo būdai: (a) įdėtos rinkiniai; b) įdėtieji skliaustai; c) koncesijų sąrašas.

Laipsniškas sąrašas turi akivaizdžių panašumų su programos kodo formatavimu. Iš tiesų, programa, parašyta pagal struktūrinio programavimo paradigmą, gali būti pavaizduota kaip medis, susidedantis iš įdėtų struktūrų.

Taip pat galite nubrėžti analogiją tarp pakopinio sąrašo ir turinio lentelių atsiradimo knygose, kur skyriuose yra poskyriai, kuriuose savo ruožtu yra poskyriai ir pan. Tradicinis tokių skyrių numeravimo būdas (1 skyrius, 1.1 ir 1.2 poskyriai, 1.1.2 poskyriai ir kt.) vadinamas Dewey dešimtaine sistema. Taikoma medžiui pav. 3 ir 4 ši sistema duos:

1. A; 1.1B; 1,2 C; 1.2.1 D; 1.2.2 E; 1.2.3 F; 1.2.3.1 G;

5.2. Pravažiuojantys medžiai

Visuose algoritmuose, susijusiuose su medžio struktūromis, visada atsiranda ta pati idėja, būtent idėja praeinant arba medžio perėjimas. Tai būdas aplankyti medžio mazgus, kai kiekvienas mazgas perkeliamas tiksliai vieną kartą. Tai lemia linijinį medžio mazgų išdėstymą. Visų pirma, yra trys būdai: galite eiti per mazgus pirmyn, atgal ir pabaigos tvarka.

Pirmyn judėjimo algoritmas:

Eikite į šaknį
Eikite per visus pomedžius iš kairės į dešinę tiesiogine tvarka.

Šis algoritmas yra rekursyvus, nes medžio perėjimas apima pomedžius, o jie, savo ruožtu, yra kertami naudojant tą patį algoritmą.

Visų pirma, medžiui pav. 3 ir 4, tiesioginis perėjimas suteikia mazgų seką: A, B, C, D, E, F, G.

Gauta seka atitinka iš kairės į dešinę nukreiptą mazgų sąrašą, kai medis vaizduojamas naudojant įdėtuosius skliaustus ir naudojant Dewey dešimtainį žymėjimą, taip pat ištrauką iš viršaus į apačią, kai jis pateikiamas kaip laipsniškas sąrašas.

Diegiant šį algoritmą programavimo kalba, pataikymas į šaknį atitinka tam tikrus veiksmus atliekančią procedūrą ar funkciją, o ėjimas per pomedžius – rekursinius skambučius į save. Visų pirma, dvejetainio medžio (kur kiekvienas mazgas turi daugiausia du pomedžius) atitinkama procedūra atrodytų taip:

// Preorder Traversal – angliškas tiesioginio užsakymo procedūros pavadinimas PreorderTraversal((Arguments)); begin //Šaknies perdavimas DoSomething((Argumentai)); //Peržengiant kairįjį pomedį if (Yra kairysis pomedis) then PreorderTransversal((2 argumentai)); //Transversal of the right submee if (Yra dešinysis pomedis) then PreorderTransversal((3 argumentai)); galas;

Tai yra, pirmiausia procedūra atlieka visus veiksmus, o tik tada įvyksta visi rekursiniai skambučiai.

Atvirkštinio judėjimo algoritmas:

Eikite per kairįjį pomedį,
Eikite į šaknį
Eikite per kitą pomedį į kairę.
Eikite į šaknį
ir tt, kol bus perkeltas dešinysis pomedis.

Tai yra, visi pomedžiai yra kertami iš kairės į dešinę, o grįžimas į šaknį yra tarp šių perėjimų. Medžiui pav. 3 ir 4 tai suteikia mazgų seką: B, A, D, C, E, G, F.

Atitinkamoje rekursyvinėje procedūroje veiksmai bus išdėstyti tarpuose tarp rekursinių skambučių. Konkrečiai dvejetainiam medžiui:

// Inorder Traversal – angliškas atvirkštinės tvarkos procedūros pavadinimas InorderTraversal((Arguments)); begin //Keliojimas kairiuoju pomedžiu if (Kairysis pomedis egzistuoja) then InorderTraversal((2 argumentai)); //Šaknies perdavimas DoSomething((Argumentai)); //Pereikite dešinįjį pomedį if (Egzistuoja dešinysis pomedis) then InorderTraversal((3 argumentai)); galas;

Užsakymo pabaigos algoritmas:

Eikite per visus pomedžius iš kairės į dešinę,
Eikite į šaknį.

Medžiui pav. 3 ir 4 tai suteiks mazgų seką: B, D, E, G, F, C, A.

Atitinkamoje rekursinėje procedūroje veiksmai bus nustatyti po rekursinių skambučių. Konkrečiai dvejetainiam medžiui:

// Postorder Traversal – angliškas galutinio užsakymo procedūros pavadinimas PostorderTraversal((Arguments)); begin //Keliavimas kairiuoju pomedžiu if (Yra kairysis pomedis) then PostorderTraversal((2 argumentai)); //Peržengiant dešinįjį pomedį if (Yra dešinysis pomedis) then PostorderTraversal((3 argumentai)); //Šaknies perdavimas DoSomething((Argumentai)); galas;

5.3. Medžio vaizdavimas kompiuterio atmintyje

Jei tam tikra informacija yra medžio mazguose, tada jai saugoti galima naudoti atitinkamą dinaminę duomenų struktūrą. Pascal tai daroma naudojant įrašo tipo kintamąjį, kuriame yra rodyklės į to paties tipo pomedžius. Pavyzdžiui, dvejetainis medis, kuriame kiekviename mazge yra sveikasis skaičius, gali būti saugomas naudojant PTree tipo kintamąjį, kuris aprašytas toliau:

Įveskite PTree = ^TTree; TTree = įrašas Inf: sveikasis skaičius; LeftSubTree, RightSubTree: PTree; galas;

Kiekvienas mazgas turi PTree tipą. Tai yra rodyklė, reiškianti, kad kiekvienas mazgas turi būti sukurtas iškviečiant naują procedūrą. Jei mazgas yra lapo mazgas, jo laukams LeftSubTree ir RightSubTree priskiriama reikšmė nulis. Kitu atveju LeftSubTree ir RightSubTree mazgai taip pat sukuriami naudojant naują procedūrą.

Vienas iš tokių įrašų schematiškai parodytas Fig. 5.

Ryžiai. 5. Scheminis TTmee tipo įrašo vaizdavimas. Įrašas turi tris laukus: Inf – skaičius, LeftSubTree ir RightSubTree – rodyklės į to paties TTmedžio tipo įrašus.

Iš tokių įrašų sudaryto medžio pavyzdys parodytas 6 paveiksle.

Ryžiai. 6. Medis, sudarytas iš TTree tipo įrašų. Kiekviename įraše saugomas skaičius ir dvi rodyklės, kuriose gali būti bet kuri nulis, arba kitų to paties tipo įrašų adresai.

Jei anksčiau nedirbote su struktūromis, susidedančiomis iš įrašų su nuorodomis į to paties tipo įrašus, rekomenduojame susipažinti su medžiaga apie tai.

6. Rekursinių algoritmų pavyzdžiai

6.1. Medžio piešimas

Panagrinėkime medžio piešimo algoritmą, parodytą pav. 6. Jei kiekviena eilutė laikoma mazgu, tai šis vaizdas visiškai atitinka ankstesniame skyriuje pateiktą medžio apibrėžimą.

Ryžiai. 6. Medis.

Akivaizdu, kad rekursyvinė procedūra nubrėžtų vieną liniją (kamieną iki pirmosios šakos), o tada pasikviestų nubrėžti du pomedžius. Pomedžiai skiriasi nuo juos turinčio medžio pradžios taško koordinatėmis, sukimosi kampu, kamieno ilgiu ir juose esančių šakų skaičiumi (vienu mažiau). Visi šie skirtumai turėtų būti padaryti rekursinės procedūros parametrais.

Tokios procedūros pavyzdys, parašytas Delphi, pateikiamas žemiau:

Procedure Tree(Canvas: TCanvas; //Drobė, ant kurios bus nupieštas medis x,y: išplėstas; //Šaknies koordinatės Kampas: išplėstas; //Kampas, kuriuo medis auga TrunkLength: išplėstas; //Kamieno ilgis n: sveikasis skaičius / /Atšakų skaičius (kiek dar liko //rekursinių skambučių)); var x2, y2: išplėstas; //Magistralės pabaiga (šakos taškas) begin x2:= x + TrunkLength * cos(kampas); y2:= y - TrunkLength * sin(kampas); Canvas.MoveTo(apvalus(x), apvalus(y)); Canvas.LineTo(apvalus(x2), apvalus(y2)); jei n > 1, tada prasideda medis (drobė, x2, y2, kampas+Pi/4, 0,55*kamieno ilgis, n-1); Medis (drobė, x2, y2, kampas-Pi/4, 0,55* kamieno ilgis, n-1); galas; galas;

Norėdami gauti pav. 6 ši procedūra buvo iškviesta naudojant šiuos parametrus:

Medis (1 vaizdas. Drobė, 175, 325, Pi/2, 120, 15);

Atminkite, kad piešimas atliekamas prieš rekursinius skambučius, tai yra, medis piešiamas tiesiogine tvarka.

6.2. Hanojaus bokštai

Pasak legendos Didžiojoje Banaro šventykloje, po katedra, žyminčia pasaulio vidurį, yra bronzinis diskas, ant kurio pritvirtinti 3 deimantiniai strypai, vienos uolekties aukščio ir storio kaip bitė. Seniai, pačioje laikų pradžioje, šio vienuolyno vienuoliai nusikalto prieš dievą Brahmą. Įsiutęs Brahma pastatė tris aukštus strypus ir ant vieno iš jų uždėjo 64 gryno aukso diskus, kad kiekvienas mažesnis diskas remtųsi ant didesnio. Kai tik visi 64 diskai bus perkelti iš strypo, ant kurio juos pastatė Dievas Brahma kurdamas pasaulį, į kitą strypą, bokštas kartu su šventykla pavirs dulkėmis ir pasaulis žus nuo perkūnijos.
Procesas reikalauja, kad didesnis diskas niekada neatsidurtų ant mažesnio. Vienuoliai susiduria su sunkumais: kokia tvarka jie turėtų dirbti pamainomis? Norint apskaičiuoti šią seką, jiems reikia pateikti programinę įrangą.

Nepriklausomai nuo Brahmos, šį galvosūkį XIX amžiaus pabaigoje pasiūlė prancūzų matematikas Edouardas Lucasas. Parduodama versija dažniausiai naudojo 7-8 diskus (7 pav.).

Ryžiai. 7. Dėlionė „Hanojaus bokštai“.

Tarkime, kad yra sprendimas n-1 diskas. Tada perjungimui n diskų, atlikite šiuos veiksmus:

1) Pamainos n-1 diskas.
2) Pamainos n diską ant likusio laisvo kaiščio.
3) Mes perkeliame krūvą iš n-1 diskas gautas taške (1) viršuje n-tas diskas.

Nes bylai n= 1 pertvarkymo algoritmas yra akivaizdus, tada indukcija, naudodami veiksmus (1) – (3), galime pertvarkyti bet kokį diskų skaičių.

Sukurkime rekursinę procedūrą, kuri spausdina visą pertvarkymų seką tam tikram diskų skaičiui. Kiekvieną kartą iškvietus tokią procedūrą, ji turi spausdinti informaciją apie vieną pamainą (iš algoritmo 2 punkto). Pertvarkant iš (1) ir (3) punktų, procedūra bus iškviesta, kai diskų skaičius sumažinamas vienu.

//n – diskų skaičius //a, b, c – pin numeriai. Perjungimas atliekamas iš kaiščio a, //į kaištį b su pagalbiniu kaiščiu c. procedura Hanoi(n, a, b, c: sveikasis skaičius); pradėti, jei n > 1, tada pradėti Hanoi(n-1, a, c, b); writeln(a, " -> ", b); Hanojus(n-1, c, b, a); end else writeln(a, " -> ", b); galas;

Atkreipkite dėmesį, kad rekursyviai iškviestų procedūrų rinkinys šiuo atveju sudaro medį, einamą atvirkštine tvarka.

6.3. Aritmetinių išraiškų analizė

Analizavimo užduotis yra apskaičiuoti išraiškos vertę naudojant esamą eilutę, kurioje yra aritmetinė išraiška ir žinomos į ją įtrauktų kintamųjų reikšmės.

Aritmetinių išraiškų skaičiavimo procesą galima pavaizduoti kaip dvejetainį medį. Iš tiesų, kiekvienam aritmetiniam operatoriui (+, –, *, /) reikalingi du operandai, kurie taip pat bus aritmetinės išraiškos ir atitinkamai gali būti laikomi pomedžiais. Ryžiai. 8 paveiksle parodytas medžio, atitinkančio išraišką, pavyzdys:

Ryžiai. 8. Sintaksės medis, atitinkantis aritmetinę išraišką (6).

Tokiame medyje galiniai mazgai visada bus kintamieji (čia x) arba skaitines konstantas, o visuose vidiniuose mazguose bus aritmetiniai operatoriai. Norėdami įvykdyti operatorių, pirmiausia turite įvertinti jo operandus. Taigi paveiksle esantis medis turėtų būti perkeltas terminalo tvarka. Atitinkama mazgų seka

paskambino atvirkštinis lenkiškas užrašas aritmetinė išraiška.

Kurdami sintaksės medį, turėtumėte atkreipti dėmesį į šią funkciją. Jei, pavyzdžiui, yra išraiška

o sudėjimo ir atimties operacijas skaitysime iš kairės į dešinę, tada teisingame sintaksės medyje vietoj pliuso bus minusas (9a pav.). Iš esmės šis medis atitinka išraišką. Galima palengvinti medžio kūrimą, jei išanalizuosite išraišką (8) atvirkščiai, iš dešinės į kairę. Tokiu atveju rezultatas yra medis su Fig. 9b, atitinkantis 8a medį, bet nereikalaujantis ženklų keitimo.

Panašiai iš dešinės į kairę reikia analizuoti išraiškas, kuriose yra daugybos ir padalijimo operatoriai.

Ryžiai. 9. Sintaksės medžiai išraiškai a – b + c skaitant iš kairės į dešinę (a) ir iš dešinės į kairę (b).

Šis metodas visiškai nepanaikina rekursijos. Tačiau tai leidžia apsiriboti tik vienu rekursinės procedūros iškvietimu, kurio gali pakakti, jei tikslas yra maksimaliai padidinti našumą.

7.3. Medžio mazgo nustatymas pagal jo skaičių

Šio metodo idėja yra pakeisti rekursinius skambučius paprasta kilpa, kuri bus vykdoma tiek kartų, kiek medyje yra mazgų, sudarytų naudojant rekursines procedūras. Kas tiksliai bus daroma kiekviename žingsnyje, turėtų būti nustatyta pagal žingsnio numerį. Žingsnio skaičiaus ir būtinų veiksmų palyginimas nėra banalus uždavinys ir kiekvienu atveju jį teks spręsti atskirai.

Pavyzdžiui, tarkime, kad norite tai padaryti kįdėtos kilpos nžingsniai kiekviename:

Jei i1:= nuo 0 iki n-1 daryti i2:= nuo 0 iki n-1 daryti i3:= nuo 0 iki n-1 daryti…

Jeigu k iš anksto nežinoma, neįmanoma jų aiškiai parašyti, kaip parodyta aukščiau. Naudodami 6.5 skyriuje parodytą metodą, galite gauti reikiamą įdėtųjų kilpų skaičių naudodami rekursinę procedūrą:

Procedūra NestedCycles(Indeksai: sveikųjų skaičių masyvas; n, k, gylis: sveikasis skaičius); var i: sveikasis skaičius; pradėti jei gylis

Norėdami atsikratyti rekursijos ir viską sumažinti iki vieno ciklo, atkreipkite dėmesį, kad jei sunumeruojate žingsnius radikso skaičių sistemoje n, tada kiekvienas žingsnis turi skaičių, kurį sudaro skaičiai i1, i2, i3, ... arba atitinkamos reikšmės iš masyvo Indeksai. Tai reiškia, kad skaičiai atitinka ciklo skaitiklių reikšmes. Žingsnio numeris įprastu dešimtainiu žymėjimu:

Iš viso bus žingsnių n k. Peržiūrėdami jų skaičius dešimtainėje skaičių sistemoje ir kiekvieną iš jų konvertuodami į raidžių sistemą n, gauname indekso reikšmes:

M:= round(IntPower(n, k)); jei i:= nuo 0 iki M-1, pradėkite Skaičius:= i; p:= nuo 0 iki k-1 pradėti Indeksai := Skaičius mod n; Skaičius:= Skaičius div n; galas; DoSomething (indeksai); galas;

Dar kartą pažymime, kad metodas nėra universalus ir kiekvienai užduočiai turėsite sugalvoti kažką kito.

Kontroliniai klausimai

1. Nustatykite, ką veiks šios rekursinės procedūros ir funkcijos.

(a) Ką išspausdins ši procedūra, kai iškviečiamas Rec(4)?

Procedūra Rec(a: sveikasis skaičius); pradėti writeln(a); jei a>0, tada Rec(a-1); writeln(a); galas;

(b) Kokia bus funkcijos Nod(78, 26) reikšmė?

Funkcija Nod(a, b: integer): sveikasis skaičius; pradėti jei a > b tada Linkteli:= Links(a – b, b) else if b > a then Nod:= Nod(a, b – a) else Nod:= a; galas;

c) Kas bus išspausdinta taikant toliau nurodytas procedūras, kai bus iškviečiamas A(1)?

Procedūra A(n: sveikas skaičius); procedūra B(n: sveikas skaičius); procedūra A(n: sveikasis skaičius); pradėti writeln(n); B(n-1); galas; procedūra B(n: sveikas skaičius); pradėti writeln(n); jei n

(d) Kas bus išspausdinta pagal toliau pateiktą procedūrą, kai skambinama BT(0, 1, 3)?

Procedūra BT(x: tikrasis; D, MaxD: sveikasis skaičius); pradėti, jei D = MaxD, tada writeln(x) kitaip prasideda BT(x – 1, D + 1, MaxD); BT(x + 1, D + 1, MaxD); galas; galas;

2. Ouroboros – gyvatė, kuri ryja savo uodegą (14 pav.), kai išskleidusi, turi ilgį L, skersmuo aplink galvą D, pilvo sienelės storis d. Nustatykite, kiek uodegos jis gali įsprausti į save ir kiek sluoksnių uodega bus klojama po to?

Ryžiai. 14. Išplėstas mūsųoboras.

3. Medžiui pav. 10a parodyta lankomų mazgų seka pirmyn, atgal ir pabaigoje.

4. Grafiškai pavaizduokite medį, apibrėžtą naudojant įdėtuosius skliaustus: (A(B(C, D), E), F, G).

5. Grafiškai pavaizduokite šios aritmetinės išraiškos sintaksės medį:

Parašykite šią išraišką atvirkštine lenkų raide.

6. Žemiau pateiktame grafike (15 pav.) užrašykite gretimų matricą ir dažnumo matricą.

Užduotys

1. Apskaičiavę faktorialą pakankamai daug kartų (milijoną ir daugiau), palyginkite rekursinio ir iteracinio algoritmų efektyvumą. Kiek skirsis vykdymo laikas ir kaip šis santykis priklausys nuo skaičiaus, kurio faktorialas skaičiuojamas?

2. Parašykite rekursinę funkciją, kuri patikrina, ar eilutėje skliaustai yra teisingai. Jei išdėstymas teisingas, tenkinamos šios sąlygos:

a) pradžios ir uždarymo skliaustų skaičius yra lygus.
(b) bet kurioje poroje yra anga - atitinkamas uždarymo laikiklis, skliausteliuose yra teisingai.

Neteisingo išdėstymo pavyzdžiai:)(, ())(, ())(() ir kt.

3. Eilutėje gali būti ir apvalių, ir laužtinių skliaustų. Kiekvienas atidarymo laikiklis turi atitinkamą to paties tipo uždarymo laikiklį (apvalus - apvalus, kvadratinis - kvadratas). Parašykite rekursinę funkciją, kuri patikrintų, ar šiuo atveju skliaustai yra teisingai.

Neteisingo išdėstymo pavyzdys: ([) ].

4. Taisyklingų skliaustų struktūrų, kurių ilgis yra 6, skaičius yra 5: ()()(), (())(), ()(()), ((())), (()()).
Parašykite rekursinę programą, kuri sukurtų visas įprastas 2 ilgio skliaustų struktūras n.

Pastaba: teisinga minimalaus ilgio „()“ skliaustų struktūra. Ilgesnio ilgio konstrukcijos gaunamos iš trumpesnio ilgio konstrukcijų dviem būdais:

a) jei mažesnė konstrukcija paimama skliausteliuose,
b) jei dvi mažesnės struktūros rašomos paeiliui.

5. Sukurkite procedūrą, kuri išspausdintų visas įmanomas sveikųjų skaičių permutacijas nuo 1 iki N.

6. Sukurkite procedūrą, kuri išspausdintų visus rinkinio poaibius (1, 2, ..., N).

7. Sukurkite procedūrą, kuri atspausdintų visas įmanomas natūraliojo skaičiaus N atvaizdas kaip kitų natūraliųjų skaičių sumą.

8. Sukurkite funkciją, kuri apskaičiuoja masyvo elementų sumą pagal tokį algoritmą: masyvas padalinamas per pusę, apskaičiuojamos ir sudedamos kiekvienos pusės elementų sumos. Elementų suma pusėje masyvo apskaičiuojama naudojant tą patį algoritmą, tai yra, vėl dalijant per pusę. Padalijimas vyksta tol, kol gautose masyvo dalyse yra po vieną elementą ir atitinkamai sumos apskaičiavimas tampa trivialus.

komentuoti: Šis algoritmas yra alternatyva. Realios vertės masyvų atveju paprastai leidžiamos mažesnės apvalinimo klaidos.

10. Sukurkite procedūrą, kuri nubrėžia Kocho kreivę (12 pav.).

11. Atkurkite figūrą. 16. Paveiksle kiekvienoje sekančioje iteracijoje apskritimas yra 2,5 karto mažesnis (šį koeficientą galima padaryti parametru).

Literatūra

1. D. Knutas. Kompiuterių programavimo menas. v. 1. (2.3 skirsnis „Medžiai“).
2. N. Wirth. Algoritmai ir duomenų struktūros.