Gegeben sind zwei rekursive Funktionen f und g. Rekursion und rekursive Algorithmen. Grundlegende Definitionen. Möglichkeiten, Bäume darzustellen

Zur Vorbereitung der Studierenden auf das Einheitliche Staatsexamen in Informatik und IKT wurde eine Präsentation zum Thema „Rekursive Algorithmen“ erstellt. Die Arbeit untersucht die Definition von Rekursion und liefert Beispiele für rekursiv definierte grafische Objekte. Die Präsentation enthält Methoden zur Lösung der Aufgabe Nr. 11 aus dem Entwurf der Demoversion des Einheitlichen Staatsexamens – 2015 in Informatik. Die erste Methode beinhaltet den Aufbau eines Aufrufbaums, die zweite Methode löst das Problem mithilfe der Substitutionsmethode. Es werden 4 Beispiele für die Lösung von Aufgaben mit beiden Methoden betrachtet. Die folgende Präsentation enthält 25 Trainingsübungen mit Antworten von der Website von Konstantin Polyakov.

Herunterladen:

Vorschau:

Um Präsentationsvorschauen zu nutzen, erstellen Sie ein Google-Konto und melden Sie sich an: https://accounts.google.com

Bildunterschriften:

Aufgabe Nr. 11 Einheitliches Staatsexamen (Grundniveau, Zeit - 5 Minuten) Rekursive Algorithmen. Autor – Korotun O.V., Informatiklehrer, Städtische Bildungseinrichtung „Sekundarschule Nr. 71“

Was Sie wissen müssen: Unter Rekursion versteht man die Definition, Beschreibung, Darstellung eines Objekts oder Prozesses innerhalb dieses Objekts oder Prozesses selbst, also einer Situation, in der ein Objekt ein Teil von sich selbst ist. Das Wappen der Russischen Föderation ist ein rekursiv definiertes grafisches Objekt: In der rechten Pfote des darauf abgebildeten Doppeladlers ist ein Zepter eingespannt, das mit einer kleineren Kopie des Wappens gekrönt ist. Da sich auf diesem Wappen auch ein Zepter in der rechten Pfote des Adlers befindet, ergibt sich eine unendliche Rekursion. Rekursives Wappen Russlands

In der Programmierung bedeutet Rekursion den Aufruf einer Funktion aus sich selbst heraus, direkt oder über andere Funktionen. Beispielsweise ruft Funktion A Funktion B auf und Funktion B ruft Funktion A auf. Die Anzahl der verschachtelten Aufrufe einer Funktion oder Prozedur wird als Rekursionstiefe bezeichnet. Beispiel für eine Rekursion: Wenn Sie einen Fettfleck auf Ihrem Kleid haben, machen Sie sich keine Sorgen. Ölflecken werden mit einer Alkalilösung entfernt. Die Spur der Essenz wird mit Öl entfernt.

Beispielaufgabe: Gegeben ein rekursiver Algorithmus: procedure F(n: integer); begin writeln(n); wenn n

Beispielaufgabe: Gegeben ein rekursiver Algorithmus: procedure F(n: integer); begin writeln (n) ; wenn n

Beispielaufgabe: Gegeben ein rekursiver Algorithmus: procedure F(n: integer); begin writeln(n); wenn n Folie 9

Beispielaufgabe: Gegeben ein rekursiver Algorithmus: procedure F(n: integer); begin writeln(n); wenn n Folie 10

Beispielaufgabe: Gegeben ein rekursiver Algorithmus: procedure F(n: integer); begin writeln(n); wenn n Folie 11

15 Beispiel Nr. 2: Gegeben ein rekursiver Algorithmus: procedure F(n: integer); begin writeln(n); wenn n

Beispiel Nr. 2: Gegeben ein rekursiver Algorithmus: procedure F(n: integer); begin writeln(n); wenn n Folie 13

Beispiel Nr. 3: Gegeben ein rekursiver Algorithmus: procedure F(n: integer); begin writeln("*") ; wenn n > 0, dann beginne F(n-2); F(n div 2) end end ; Wie viele Sternchen werden beim Aufruf von F(7) auf dem Bildschirm gedruckt? 7 5 3 2 3 1 1 1 1 In diesem Beispiel wird das Symbol * -2 div 2 1 0 -1 0 -1 0 -1 -1 -1 0 0 0 auf dem Bildschirm angezeigt und nicht die Werte von Parameter n .

Beispiel Nr. 3: Gegeben ein rekursiver Algorithmus: procedure F(n: integer); begin writeln("*"); wenn n > 0, dann beginne F(n-2); F(n div 2) end end ; Wie viele Sternchen werden beim Aufruf von F(7) auf dem Bildschirm gedruckt? * Wenn wir die Anzahl der „Sterne“ zählen, erhalten wir 21. In diesem Beispiel werden nicht die Werte des Parameters n auf dem Bildschirm angezeigt, sondern das Symbol * * * * * * * * * * * * * * * * * * * * * *

Beispiel Nr. 3: Gegeben ein rekursiver Algorithmus: procedure F(n: integer); begin writeln("*"); wenn n > 0, dann beginne F(n-2); F(n div 2) end end ; Wie viele Sternchen werden beim Aufruf von F(7) auf dem Bildschirm gedruckt? Lassen Sie uns das Problem ohne Baum lösen. Sei S(n) die Anzahl der „Sterne“, die beim Aufruf von F(n) gedruckt werden. Dann 1+S(n-2)+ S(n div 2), n>0 1 , n Wir müssen S(7) kennen. S(7)= 1 +S(5)+S(3) S(5)= 1 +S(3)+S(2) S(3)= 1 +S(1)+S(1) S( 2)=1+S(0)+S(1)=1+1+S(1)=2+S(1) S(1)= 1+ S(-1)+S(0)=1+ 1+1=3 Umgekehrt: S(2)=2+3=5 S(3)=1+3+3=7 S(5)=1+7+5=13 S(7)=1+ 13+ 7= 21 S(n)=

Beispiel Nr. 4: Prozedur F(n: integer); Beginnen Sie mit Folie 18

Beispiel Nr. 4: Prozedur F(n: integer); Beginnen Sie mit Folie 19

Beispiel Nr. 4: Prozedur F(n: integer); beginnen, wenn n

Trainingsaufgaben

Problem 1: Gegeben ein rekursiver Algorithmus: procedure F(n: integer); begin writeln("*"); wenn n > 0, dann beginne F(n-2); F(n div 2); F(n div 2); Ende Ende ; Wie viele Sternchen werden beim Aufruf von F(5) auf dem Bildschirm gedruckt? Antwort: 34

Problem 2: Gegeben ein rekursiver Algorithmus: procedure F(n: integer); begin writeln("*"); wenn n > 0, dann beginne F(n-2); F(n-2); F(n div 2); Ende Ende ; Wie viele Sternchen werden beim Aufruf von F(6) auf dem Bildschirm gedruckt? Antwort: 58

Problem 3: Gegeben ein rekursiver Algorithmus: procedure F(n: integer); begin writeln("*"); wenn n > 0, dann beginne F(n-3); F(n div 2); Ende Ende ; Wie viele Sternchen werden beim Aufruf von F(7) auf dem Bildschirm gedruckt? Antwort: 15

Problem 4: Gegeben ein rekursiver Algorithmus: procedure F(n: integer); begin writeln("*"); wenn n > 0, dann beginne F(n-3); F(n-2); F(n div 2); Ende Ende ; Wie viele Sternchen werden beim Aufruf von F(7) auf dem Bildschirm gedruckt? Antwort: 55

Problem 5: Gegeben ein rekursiver Algorithmus: procedure F(n: integer); begin writeln("*"); wenn n > 0, dann beginne F(n-3); F(n-2); F(n div 2); F(n div 2); Ende Ende ; Wie viele Sternchen werden beim Aufruf von F(6) auf dem Bildschirm gedruckt? Antwort: 97

Problem 6: Gegeben ein rekursiver Algorithmus: procedure F(n: integer); begin writeln("*"); wenn n > 0 dann begin writeln("*"); F(n-2); F(n div 2); Ende Ende ; Wie viele Sternchen werden beim Aufruf von F(7) auf dem Bildschirm gedruckt? Antwort: 31

Problem 7: Gegeben ein rekursiver Algorithmus: procedure F(n: integer); begin writeln("*"); wenn n > 0 dann begin writeln("*"); F(n-2); F(n div 2); F(n div 2); Ende Ende; Wie viele Sternchen werden beim Aufruf von F(7) auf dem Bildschirm gedruckt? Antwort: 81

Problem 8: Gegeben ein rekursiver Algorithmus: procedure F(n: integer); begin writeln("*"); wenn n > 0 dann begin writeln("*"); F(n-2); F(n-2); F(n div 2); Ende Ende; Wie viele Sternchen werden beim Aufruf von F(6) auf dem Bildschirm gedruckt? Antwort: 77

Problem 9: Gegeben ein rekursiver Algorithmus: procedure F(n: integer); beginnen, wenn n > 0, dann beginnen F(n-2); F(n-1); F(n-1); Ende; writeln("*"); Ende ; Wie viele Sternchen werden beim Aufruf von F(5) auf dem Bildschirm gedruckt? Antwort: 148

Problem 10: Gegeben ein rekursiver Algorithmus: procedure F(n: integer); begin if n > 0 then begin writeln("*"); F(n-2); F(n-1); F(n-1); Ende; writeln("*"); Ende; Wie viele Sternchen werden beim Aufruf von F(5) auf dem Bildschirm gedruckt? Antwort: 197

Problem 11: Gegeben ein rekursiver Algorithmus: procedure F(n: integer); beginnen, wenn n > 1, dann beginnen F(n-2); F(n-1); F(n div 2); Ende; writeln("*"); Ende ; Wie viele Sternchen werden beim Aufruf von F(7) auf dem Bildschirm gedruckt? Antwort: 88

Problem 12: Gegeben ein rekursiver Algorithmus: procedure F(n: integer); begin if n > 2 then begin writeln("*"); F(n-2); F(n-1); F(n div 2); Ende ; writeln("*"); Ende; Wie viele Sternchen werden beim Aufruf von F(6) auf dem Bildschirm gedruckt? Antwort: 33

Problem 13: Gegeben ein rekursiver Algorithmus: Prozedur F (n: Ganzzahl); begin writeln(n); wenn n

Problem 14: Gegeben ein rekursiver Algorithmus: Prozedur F (n: Ganzzahl); begin writeln(n); wenn n

Problem 15: Gegeben ein rekursiver Algorithmus: Prozedur F (n: Ganzzahl); begin writeln(n); wenn n

Problem 16: Gegeben ein rekursiver Algorithmus: Prozedur F (n: Ganzzahl); beginne writeln(n); wenn n

Problem 17: Gegeben ein rekursiver Algorithmus: Prozedur F (n: Ganzzahl); begin writeln(n); wenn n

Problem 18: Gegeben ein rekursiver Algorithmus: Prozedur F (n: Ganzzahl); begin writeln(n); wenn n

Problem 19: Gegeben ein rekursiver Algorithmus: Prozedur F (n: Ganzzahl); begin writeln(n); wenn n

Problem 20: Gegeben ein rekursiver Algorithmus: Prozedur F (n: Ganzzahl); begin writeln(n); wenn n

Problem 21: Gegeben ein rekursiver Algorithmus: Prozedur F (n: Ganzzahl); beginne writeln(n); wenn n

Problem 22: Gegeben ein rekursiver Algorithmus: Prozedur F (n: Ganzzahl); beginne writeln(n); wenn n

Problem 23: Gegeben ein rekursiver Algorithmus: Prozedur F (n: Ganzzahl); beginne writeln(n); wenn n

Problem 24: Gegeben ein rekursiver Algorithmus: Prozedur F (n: Ganzzahl); begin writeln(n); wenn n

Problem 25: Gegeben ein rekursiver Algorithmus: Prozedur F (n: Ganzzahl); begin writeln(n); wenn n

Von einer Rekursion spricht man, wenn sich ein Unterprogramm selbst aufruft. Wenn man zum ersten Mal mit einem solchen algorithmischen Design konfrontiert wird, stoßen die meisten Menschen auf gewisse Schwierigkeiten, aber mit ein wenig Übung wird die Rekursion zu einem verständlichen und sehr nützlichen Werkzeug in Ihrem Programmierarsenal.

1. Das Wesen der Rekursion

Eine Prozedur oder Funktion kann Aufrufe anderer Prozeduren oder Funktionen enthalten. Die Prozedur kann sich auch selbst aufrufen. Hier liegt kein Paradoxon vor: Der Computer führt die Befehle, auf die er im Programm stößt, nur nacheinander aus, und wenn er auf einen Prozeduraufruf stößt, beginnt er einfach mit der Ausführung dieser Prozedur. Es spielt keine Rolle, welche Prozedur den Befehl dazu gegeben hat.

Beispiel für ein rekursives Verfahren:

Prozedur Rec(a: integer); begin if a>

Betrachten wir, was passiert, wenn im Hauptprogramm beispielsweise ein Aufruf der Form Rec(3) erfolgt. Nachfolgend finden Sie ein Flussdiagramm, das die Ausführungssequenz der Anweisungen zeigt.

Reis. 1. Blockdiagramm des rekursiven Verfahrens.

Die Prozedur Rec wird mit dem Parameter a = 3 aufgerufen. Sie enthält einen Aufruf der Prozedur Rec mit dem Parameter a = 2. Der vorherige Aufruf ist noch nicht abgeschlossen, Sie können sich also vorstellen, dass eine weitere Prozedur erstellt wird und die erste ihre Arbeit erst beendet es endet. Der aufrufende Prozess endet, wenn Parameter a = 0. Zu diesem Zeitpunkt werden 4 Instanzen der Prozedur gleichzeitig ausgeführt. Man nennt die Anzahl gleichzeitig durchgeführter Vorgänge Rekursionstiefe.

Die vierte Prozedur namens (Rec(0)) gibt die Zahl 0 aus und beendet ihre Arbeit. Danach kehrt die Steuerung zu der Prozedur zurück, die sie aufgerufen hat (Rec(1)), und die Nummer 1 wird ausgegeben. Und so weiter, bis alle Prozeduren abgeschlossen sind. Der ursprüngliche Anruf gibt vier Zahlen aus: 0, 1, 2, 3.

Ein weiteres visuelles Bild dessen, was passiert, ist in Abb. dargestellt. 2.

Reis. 2. Die Ausführung der Rec-Prozedur mit Parameter 3 besteht aus der Ausführung der Rec-Prozedur mit Parameter 2 und dem Ausdrucken der Zahl 3. Die Ausführung der Rec-Prozedur mit Parameter 2 wiederum besteht aus der Ausführung der Rec-Prozedur mit Parameter 1 und dem Ausdrucken der Zahl 2 usw .

Überlegen Sie als eigene Übung, was passiert, wenn Sie Rec(4) aufrufen. Bedenken Sie auch, was passieren würde, wenn Sie die folgende Rec2(4)-Prozedur mit umgekehrten Operatoren aufrufen würden.

Prozedur Rec2(a: Ganzzahl); beginne writeln(a); wenn a>0 dann Rec2(a-1); Ende;

Bitte beachten Sie, dass in diesen Beispielen der rekursive Aufruf innerhalb einer bedingten Anweisung erfolgt. Dies ist eine notwendige Voraussetzung dafür, dass die Rekursion jemals endet. Beachten Sie außerdem, dass sich die Prozedur selbst mit einem anderen Parameter aufruft als dem, mit dem sie aufgerufen wurde. Wenn das Verfahren keine globalen Variablen verwendet, ist dies auch notwendig, damit die Rekursion nicht unendlich weitergeht.

Ein etwas komplexeres Schema ist möglich: Funktion A ruft Funktion B auf, die wiederum A aufruft. Dies wird aufgerufen komplexe Rekursion. Es stellt sich heraus, dass die zuerst beschriebene Prozedur eine noch nicht beschriebene Prozedur aufrufen muss. Damit dies möglich ist, müssen Sie verwenden.

Prozedur A(n: Ganzzahl); (Vorwärtsbeschreibung (Header) der ersten Prozedur) procedure B(n: integer); (Vorwärtsbeschreibung der zweiten Prozedur) procedure A(n: integer); (Vollständige Beschreibung der Prozedur A) begin writeln(n); B(n-1); Ende; Prozedur B(n: ganze Zahl); (Vollständige Beschreibung von Prozedur B) begin writeln(n); wenn n

Die Vorwärtsdeklaration von Prozedur B ermöglicht den Aufruf von Prozedur A. Die Vorwärtsdeklaration von Prozedur A ist in diesem Beispiel nicht erforderlich und wird aus ästhetischen Gründen hinzugefügt.

Wenn eine gewöhnliche Rekursion mit einem Ouroboros verglichen werden kann (Abb. 3), dann kann das Bild einer komplexen Rekursion aus dem berühmten Kindergedicht abgeleitet werden, in dem „Die Wölfe hatten Angst und fraßen sich gegenseitig.“ Stellen Sie sich zwei Wölfe vor, die sich gegenseitig fressen, und Sie werden die komplexe Rekursion verstehen.

Reis. 3. Ouroboros – eine Schlange, die ihren eigenen Schwanz verschlingt. Zeichnung aus der alchemistischen Abhandlung „Synosius“ von Theodore Pelecanos (1478).

Reis. 4. Komplexe Rekursion.

3. Simulation einer Schleife mittels Rekursion

Wenn sich eine Prozedur selbst aufruft, führt sie im Wesentlichen dazu, dass die darin enthaltenen Anweisungen erneut ausgeführt werden, ähnlich einer Schleife. Einige Programmiersprachen enthalten überhaupt keine Schleifenkonstrukte, sodass Programmierer Wiederholungen mithilfe von Rekursion organisieren müssen (z. B. Prolog, wo Rekursion eine grundlegende Programmiertechnik ist).

Lassen Sie uns beispielsweise den Betrieb einer for-Schleife simulieren. Dazu benötigen wir eine Schrittzählervariable, die beispielsweise als Prozedurparameter implementiert werden kann.

Beispiel 1.

Prozedur LoopImitation(i, n: integer); (Der erste Parameter ist der Schrittzähler, der zweite Parameter ist die Gesamtzahl der Schritte) begin writeln("Hello N ", i); //Hier sind alle Anweisungen, die wiederholt werden, wenn i

Das Ergebnis eines Aufrufs der Form LoopImitation(1, 10) ist die zehnmalige Ausführung von Anweisungen, wodurch sich der Zähler von 1 auf 10 ändert. In diesem Fall wird Folgendes gedruckt:

Hallo N1
Hallo N2
…
Hallo N 10

Im Allgemeinen ist es nicht schwer zu erkennen, dass die Parameter des Verfahrens die Grenzen für die Änderung der Zählerwerte darstellen.

Sie können den rekursiven Aufruf und die zu wiederholenden Anweisungen wie im folgenden Beispiel vertauschen.

Beispiel 2.

Prozedur LoopImitation2(i, n: integer); beginnen, wenn ich

In diesem Fall erfolgt ein rekursiver Prozeduraufruf, bevor mit der Ausführung der Anweisungen begonnen wird. Die neue Instanz der Prozedur ruft zunächst auch eine andere Instanz auf und so weiter, bis wir den Maximalwert des Zählers erreichen. Erst danach führt die letzte der aufgerufenen Prozeduren ihre Anweisungen aus, dann führt die vorletzte ihre Anweisungen aus usw. Das Ergebnis des Aufrufs von LoopImitation2(1, 10) ist, dass Begrüßungen in umgekehrter Reihenfolge gedruckt werden:

Hallo N 10
…
Hallo N1

Wenn wir uns eine Kette rekursiv aufgerufener Prozeduren vorstellen, dann durchlaufen wir diese in Beispiel 1 von früher aufgerufenen Prozeduren zu späteren. Im Beispiel 2 hingegen von später nach früher.

Schließlich kann ein rekursiver Aufruf zwischen zwei Befehlsblöcken platziert werden. Zum Beispiel:

Prozedur LoopImitation3(i, n: integer); begin writeln("Hallo N", i); (Der erste Anweisungsblock befindet sich möglicherweise hier) wenn i

Dabei werden zunächst die Anweisungen aus dem ersten Block sequentiell ausgeführt, anschließend werden die Anweisungen aus dem zweiten Block in umgekehrter Reihenfolge ausgeführt. Beim Aufruf von LoopImitation3(1, 10) erhalten wir:

Hallo N1
…
Hallo N 10
Hallo N 10
…
Hallo N1

Ohne Rekursion wären zwei Schleifen erforderlich, um dasselbe zu tun.

Sie können sich die Tatsache zunutze machen, dass die Ausführung von Teilen derselben Prozedur zeitlich versetzt erfolgt. Zum Beispiel:

Beispiel 3: Konvertieren einer Zahl in eine Binärzahl.

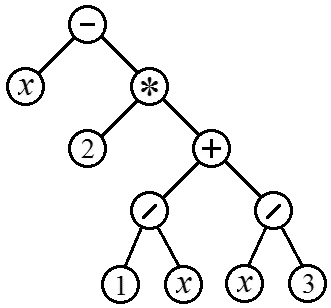
Die Ermittlung der Ziffern einer Binärzahl erfolgt bekanntlich durch Division mit einem Rest durch die Basis des Zahlensystems 2. Wenn es eine Zahl gibt, dann ist ihre letzte Ziffer in ihrer Binärdarstellung gleich

Den ganzzahligen Teil aus der Division durch 2 ziehen:

wir erhalten eine Zahl, die dieselbe binäre Darstellung hat, jedoch ohne die letzte Ziffer. Somit reicht es aus, die beiden oben genannten Operationen zu wiederholen, bis das nächste Divisionsfeld einen ganzzahligen Teil gleich 0 erhält. Ohne Rekursion sieht es so aus:

While x>0 do begin c:=x mod 2; x:=x div 2; write(c); Ende;

Das Problem hierbei ist, dass die Ziffern der Binärdarstellung in umgekehrter Reihenfolge (neueste zuerst) berechnet werden. Um eine Zahl in Normalform auszugeben, müssen Sie sich alle Zahlen in den Array-Elementen merken und sie in einer separaten Schleife ausdrucken.

Mithilfe der Rekursion ist es nicht schwierig, ohne ein Array und eine zweite Schleife eine Ausgabe in der richtigen Reihenfolge zu erreichen. Nämlich:

Prozedur BinaryRepresentation(x: integer); var c, x: Ganzzahl; begin (Erster Block. Wird in der Reihenfolge der Prozeduraufrufe ausgeführt) c:= x mod 2; x:= x div 2; (Rekursiver Aufruf) if x>0 then BinaryRepresentation(x); (Zweiter Block. Wird in umgekehrter Reihenfolge ausgeführt) write(c); Ende;

Generell haben wir keine Gewinne erhalten. Die Ziffern der Binärdarstellung werden in lokalen Variablen gespeichert, die für jede laufende Instanz der rekursiven Prozedur unterschiedlich sind. Das heißt, es war nicht möglich, Speicher zu sparen. Im Gegenteil, wir verschwenden zusätzlichen Speicher für die Speicherung vieler lokaler Variablen x. Diese Lösung erscheint mir jedoch schön.

4. Wiederholungsbeziehungen. Rekursion und Iteration

Eine Folge von Vektoren heißt durch eine Rekursionsrelation gegeben, wenn der Anfangsvektor und die funktionale Abhängigkeit des nachfolgenden Vektors vom vorherigen gegeben sind

Ein einfaches Beispiel für eine mithilfe von Wiederholungsrelationen berechnete Größe ist die Fakultät

Die nächste Fakultät kann aus der vorherigen wie folgt berechnet werden:

Durch Einführung der Notation erhalten wir die Beziehung:

Die Vektoren aus Formel (1) können als Mengen variabler Werte interpretiert werden. Dann besteht die Berechnung des erforderlichen Elements der Sequenz aus der wiederholten Aktualisierung ihrer Werte. Insbesondere für Fakultäten:

X:= 1; for i:= 2 to n do x:= x * i; writeln(x);

Jedes dieser Updates (x:= x * i) wird aufgerufen Wiederholung und der Prozess der Wiederholung von Iterationen ist Wiederholung.

Beachten wir jedoch, dass Relation (1) eine rein rekursive Definition der Folge ist und die Berechnung des n-ten Elements tatsächlich die wiederholte Übernahme der Funktion f aus sich selbst ist:

Insbesondere für Fakultät kann man schreiben:

Funktion Factorial(n: integer): integer; begin if n > 1 then Factorial:= n * Factorial(n-1) else Factorial:= 1; Ende;

Es sollte klar sein, dass das Aufrufen von Funktionen einen gewissen zusätzlichen Aufwand mit sich bringt, sodass die erste Option zur Berechnung der Fakultät etwas schneller ist. Im Allgemeinen funktionieren iterative Lösungen schneller als rekursive.

Bevor wir zu Situationen übergehen, in denen Rekursion nützlich ist, schauen wir uns ein weiteres Beispiel an, in dem sie nicht verwendet werden sollte.

Betrachten wir einen Sonderfall wiederkehrender Beziehungen, bei dem der nächste Wert in der Folge nicht von einem, sondern von mehreren vorherigen Werten gleichzeitig abhängt. Ein Beispiel ist die berühmte Fibonacci-Folge, bei der jedes nächste Element die Summe der beiden vorherigen ist:

Mit einem „frontalen“ Ansatz können Sie schreiben:

Funktion Fib(n: integer): integer; begin if n > 1 then Fib:= Fib(n-1) + Fib(n-2) else Fib:= 1; Ende;

Jeder Fib-Aufruf erstellt zwei Kopien von sich selbst, jede Kopie erstellt zwei weitere und so weiter. Die Anzahl der Operationen steigt mit der Anzahl N exponentiell, allerdings mit einer iterativen Lösung linear in N Anzahl der Operationen.

Tatsächlich lehrt uns das obige Beispiel, dass dies nicht der Fall ist WANN Andernfalls sollte die Rekursion nicht verwendet werden WIE es sollte nicht verwendet werden. Wenn es schließlich eine schnelle iterative (schleifenbasierte) Lösung gibt, kann dieselbe Schleife mithilfe einer rekursiven Prozedur oder Funktion implementiert werden. Zum Beispiel:

// x1, x2 – Anfangsbedingungen (1, 1) // n – Nummer der erforderlichen Fibonacci-Zahlenfunktion Fib(x1, x2, n: integer): integer; var x3: Ganzzahl; begin if n > 1 then begin x3:= x2 + x1; x1:= x2; x2:= x3; Fib:= Fib(x1, x2, n-1); end else Fib:= x2; Ende;

Dennoch sind iterative Lösungen vorzuziehen. Es stellt sich die Frage: Wann sollte in diesem Fall die Rekursion verwendet werden?

Alle rekursiven Prozeduren und Funktionen, die nur einen rekursiven Aufruf an sich selbst enthalten, können leicht durch iterative Schleifen ersetzt werden. Um etwas zu erhalten, für das es kein einfaches nichtrekursives Gegenstück gibt, müssen Sie auf Prozeduren und Funktionen zurückgreifen, die sich selbst zwei- oder mehrmals aufrufen. In diesem Fall bildet die Menge der aufgerufenen Prozeduren keine Kette mehr, wie in Abb. 1, aber ein ganzer Baum. Es gibt zahlreiche Problemklassen, bei denen der Rechenprozess auf diese Weise organisiert werden muss. Für sie wird die Rekursion die einfachste und natürlichste Lösung sein.

5. Bäume

Die theoretische Grundlage für rekursive Funktionen, die sich selbst mehr als einmal aufrufen, ist der Zweig der diskreten Mathematik, der Bäume untersucht.

5.1. Grundlegende Definitionen. Möglichkeiten, Bäume darzustellen

Definition: Wir nennen die endliche Menge T, bestehend aus einem oder mehreren Knoten, so dass:
a) Es gibt einen speziellen Knoten namens Wurzel dieses Baums.
b) Die übrigen Knoten (mit Ausnahme der Wurzel) sind in paarweise disjunkten Teilmengen enthalten, von denen jede wiederum ein Baum ist. Bäume werden gerufen Teilbäume dieses Baumes.

Diese Definition ist rekursiv. Kurz gesagt ist ein Baum eine Menge bestehend aus einer Wurzel und daran befestigten Teilbäumen, die ebenfalls Bäume sind. Ein Baum definiert sich durch sich selbst. Diese Definition ist jedoch sinnvoll, da die Rekursion endlich ist. Jeder Teilbaum enthält weniger Knoten als der Baum, der ihn enthält. Am Ende kommen wir zu Teilbäumen, die nur einen Knoten enthalten, und hier ist bereits klar, um was es sich handelt.

Reis. 3. Baum.

In Abb. Abbildung 3 zeigt einen Baum mit sieben Knoten. Obwohl gewöhnliche Bäume von unten nach oben wachsen, ist es üblich, sie umgekehrt zu zeichnen. Wenn Sie ein Diagramm von Hand zeichnen, ist diese Methode offensichtlich bequemer. Aufgrund dieser Inkonsistenz kommt es manchmal zu Verwirrung, wenn gesagt wird, dass ein Knoten über oder unter einem anderen liegt. Aus diesem Grund ist es bequemer, die bei der Beschreibung von Stammbäumen verwendete Terminologie zu verwenden und Knoten näher an der Wurzel als Vorfahren und weiter entfernte Knoten als Nachkommen zu bezeichnen.

Ein Baum kann auf andere Weise grafisch dargestellt werden. Einige davon sind in Abb. dargestellt. 4. Laut Definition ist ein Baum ein System verschachtelter Mengen, wobei sich diese Mengen entweder nicht schneiden oder vollständig ineinander enthalten sind. Solche Mengen können als Regionen auf einer Ebene dargestellt werden (Abb. 4a). In Abb. In 4b liegen die verschachtelten Mengen nicht auf einer Ebene, sondern sind zu einer Linie verlängert. Reis. 4b kann auch als Diagramm einer algebraischen Formel mit verschachtelten Klammern betrachtet werden. Reis. Abbildung 4c zeigt eine weitere beliebte Möglichkeit, eine Baumstruktur als gestaffelte Liste darzustellen.

Reis. 4. Andere Möglichkeiten, Baumstrukturen darzustellen: (a) verschachtelte Mengen; (b) verschachtelte Klammern; (c) Konzessionsliste.

Die gestaffelte Liste weist offensichtliche Ähnlichkeiten mit der Formatierung des Programmcodes auf. Tatsächlich kann ein im Rahmen des strukturierten Programmierparadigmas geschriebenes Programm als Baum dargestellt werden, der aus verschachtelten Strukturen besteht.

Sie können auch eine Analogie zwischen der Stufenliste und dem Erscheinungsbild von Inhaltsverzeichnissen in Büchern ziehen, in denen Abschnitte Unterabschnitte enthalten, die wiederum Unterabschnitte usw. enthalten. Die traditionelle Art der Nummerierung solcher Abschnitte (Abschnitt 1, Unterabschnitte 1.1 und 1.2, Unterabschnitt 1.1.2 usw.) wird als Dewey-Dezimalsystem bezeichnet. Auf den Baum in Abb. angewendet. 3 und 4 ergibt dieses System:

1. A; 1,1B; 1,2 °C; 1.2.1 D; 1.2.2 E; 1,2,3 F; 1.2.3.1 G;

5.2. Vorbeiziehende Bäume

In allen Algorithmen, die sich auf Baumstrukturen beziehen, taucht immer dieselbe Idee auf, nämlich die Idee Vorbeigehen oder Baumdurchquerung. Dies ist eine Möglichkeit, Baumknoten zu besuchen, bei der jeder Knoten genau einmal durchlaufen wird. Dies führt zu einer linearen Anordnung der Baumknoten. Insbesondere gibt es drei Möglichkeiten: Sie können die Knoten in Vorwärts-, Rückwärts- und Endreihenfolge durchlaufen.

Vorwärtsdurchquerungsalgorithmus:

Gehen Sie der Wurzel auf den Grund
Gehen Sie alle Teilbäume von links nach rechts in direkter Reihenfolge durch.

Dieser Algorithmus ist rekursiv, da die Durchquerung eines Baums die Durchquerung von Teilbäumen beinhaltet und diese wiederum mit demselben Algorithmus durchquert werden.

Insbesondere für den Baum in Abb. 3 und 4, direkte Durchquerung ergibt eine Folge von Knoten: A, B, C, D, E, F, G.

Die resultierende Sequenz entspricht einer Aufzählung von Knoten von links nach rechts, wenn ein Baum mit verschachtelten Klammern und in der Dewey-Dezimalschreibweise dargestellt wird, sowie einem Durchgang von oben nach unten, wenn er als gestaffelte Liste dargestellt wird.

Bei der Implementierung dieses Algorithmus in einer Programmiersprache entspricht das Erreichen der Wurzel der Prozedur oder Funktion, die einige Aktionen ausführt, und das Durchlaufen von Teilbäumen entspricht rekursiven Aufrufen an sich selbst. Insbesondere für einen Binärbaum (bei dem jeder Knoten höchstens zwei Teilbäume hat) würde die entsprechende Vorgehensweise folgendermaßen aussehen:

// Preorder Traversal – Englischer Name für das direkte Bestellverfahren PreorderTraversal((Arguments)); begin //Übergabe der Wurzel DoSomething((Arguments)); //Übergang des linken Teilbaums if (Es gibt einen linken Teilbaum) then PreorderTransversal((Argumente 2)); //Transversal des rechten Teilbaums if (Es gibt einen rechten Teilbaum) then PreorderTransversal((Argumente 3)); Ende;

Das heißt, die Prozedur führt zunächst alle Aktionen aus und erst dann erfolgen alle rekursiven Aufrufe.

Reverse-Traversal-Algorithmus:

Gehen Sie durch den linken Teilbaum,
Gehen Sie der Wurzel auf den Grund
Gehen Sie durch den nächsten Teilbaum nach links.
Gehen Sie der Wurzel auf den Grund
usw., bis der Teilbaum ganz rechts durchlaufen wird.

Das heißt, alle Teilbäume werden von links nach rechts durchlaufen, und die Rückkehr zur Wurzel befindet sich zwischen diesen Durchläufen. Für den Baum in Abb. 3 und 4 ergibt die Reihenfolge der Knoten: B, A, D, C, E, G, F.

Bei einem entsprechenden rekursiven Verfahren liegen die Aktionen in den Zwischenräumen zwischen den rekursiven Aufrufen. Speziell für einen Binärbaum:

// Inorder Traversal – Englischer Name für die Prozedur in umgekehrter Reihenfolge InorderTraversal((Arguments)); begin //Durch den linken Teilbaum reisen if (There is a left subtree) then InorderTraversal((Arguments 2)); //Übergabe der Wurzel DoSomething((Arguments)); //Den rechten Teilbaum durchqueren if (Ein rechter Teilbaum existiert) then InorderTraversal((Argumente 3)); Ende;

End-Order-Traversal-Algorithmus:

Gehen Sie alle Teilbäume von links nach rechts durch,
Gehen Sie der Wurzel auf den Grund.

Für den Baum in Abb. 3 und 4 ergibt die Reihenfolge der Knoten: B, D, E, G, F, C, A.

Bei einem entsprechenden rekursiven Verfahren werden die Aktionen nach den rekursiven Aufrufen angeordnet. Speziell für einen Binärbaum:

// Postorder Traversal – Englischer Name für die End-Order-Prozedur PostorderTraversal((Arguments)); begin //Durch den linken Teilbaum reisen if (Es gibt einen linken Teilbaum) then PostorderTraversal((Argumente 2)); //Transzendieren des rechten Teilbaums if (A right subtree existed) then PostorderTraversal((Argumente 3)); //Übergabe der Wurzel DoSomething((Arguments)); Ende;

5.3. Darstellung eines Baumes im Computerspeicher

Wenn sich einige Informationen in Baumknoten befinden, kann eine entsprechende dynamische Datenstruktur zum Speichern dieser Informationen verwendet werden. In Pascal erfolgt dies mithilfe einer Datensatztypvariablen, die Zeiger auf Teilbäume desselben Typs enthält. Beispielsweise kann ein Binärbaum, in dem jeder Knoten eine Ganzzahl enthält, mithilfe einer Variablen vom Typ PTree gespeichert werden, was im Folgenden beschrieben wird:

Typ PTree = ^TTree; TTree = Datensatz Inf: Ganzzahl; LeftSubTree, RightSubTree: PTree; Ende;

Jeder Knoten hat einen PTree-Typ. Dies ist ein Zeiger, was bedeutet, dass jeder Knoten durch Aufrufen der New-Prozedur erstellt werden muss. Wenn der Knoten ein Blattknoten ist, wird seinen Feldern LeftSubTree und RightSubTree der Wert zugewiesen Null. Andernfalls werden die Knoten LeftSubTree und RightSubTree auch durch die New-Prozedur erstellt.

Eine solche Aufzeichnung ist schematisch in Abb. dargestellt. 5.

Reis. 5. Schematische Darstellung eines Datensatzes vom Typ TTree. Der Datensatz hat drei Felder: Inf – eine Zahl, LeftSubTree und RightSubTree – Zeiger auf Datensätze desselben TTree-Typs.

Ein Beispiel für einen Baum, der aus solchen Datensätzen besteht, ist in Abbildung 6 dargestellt.

Reis. 6. Ein Baum, der aus Datensätzen vom Typ TTree besteht. Jeder Eintrag speichert eine Zahl und zwei Zeiger, die beides enthalten können Null oder Adressen anderer Datensätze desselben Typs.

Wenn Sie noch nicht mit Strukturen gearbeitet haben, die aus Datensätzen bestehen, die Links zu Datensätzen desselben Typs enthalten, empfehlen wir Ihnen, sich mit dem Material darüber vertraut zu machen.

6. Beispiele für rekursive Algorithmen

6.1. Einen Baum zeichnen

Betrachten wir den Algorithmus zum Zeichnen des in Abb. gezeigten Baums. 6. Wenn jede Linie als Knoten betrachtet wird, erfüllt dieses Bild vollständig die im vorherigen Abschnitt angegebene Definition eines Baums.

Reis. 6. Baum.

Die rekursive Prozedur würde offensichtlich eine Linie zeichnen (den Stamm bis zum ersten Zweig) und sich dann selbst aufrufen, um die beiden Teilbäume zu zeichnen. Teilbäume unterscheiden sich von dem Baum, der sie enthält, durch die Koordinaten ihres Startpunkts, den Rotationswinkel, die Stammlänge und die Anzahl der Zweige, die sie enthalten (einen weniger). Alle diese Unterschiede sollten zu Parametern des rekursiven Verfahrens gemacht werden.

Ein Beispiel für eine solche Prozedur, geschrieben in Delphi, ist unten dargestellt:

Procedure Tree(Canvas: TCanvas; //Canvas, auf dem der Baum gezeichnet wird x,y: erweitert; //Wurzelkoordinaten Winkel: erweitert; //Winkel, in dem der Baum wächst TrunkLength: erweitert; //Stammlänge n: Ganzzahl //Anzahl der Verzweigungen (wie viele weitere //rekursive Aufrufe verbleiben)); var x2, y2: erweitert; //Trunk-Ende (Verzweigungspunkt) beginnt x2:= x + TrunkLength * cos(Angle); y2:= y - TrunkLength * sin(Winkel); Canvas.MoveTo(round(x), Round(y)); Canvas.LineTo(round(x2), Round(y2)); Wenn n > 1, dann begin Tree(Canvas, x2, y2, Angle+Pi/4, 0.55*TrunkLength, n-1); Baum (Leinwand, x2, y2, Winkel-Pi/4, 0,55 * Stammlänge, n-1); Ende; Ende;

Um Abb. 6 wurde diese Prozedur mit den folgenden Parametern aufgerufen:

Baum(Image1.Canvas, 175, 325, Pi/2, 120, 15);

Beachten Sie, dass das Zeichnen vor rekursiven Aufrufen erfolgt, d. h. der Baum wird in direkter Reihenfolge gezeichnet.

6.2. Hanoi-Türme

Der Legende nach befindet sich im Großen Tempel von Banaras unter der Kathedrale, die die Mitte der Welt markiert, eine Bronzescheibe, auf der drei Diamantstäbe befestigt sind, eine Elle hoch und dick wie eine Biene. Vor langer Zeit, ganz am Anfang der Zeit, begingen die Mönche dieses Klosters Anstoß gegen den Gott Brahma. Wütend errichtete Brahma drei hohe Stäbe und legte 64 Scheiben aus reinem Gold auf einen von ihnen, sodass jede kleinere Scheibe auf einer größeren ruhte. Sobald alle 64 Scheiben von dem Stab, auf den Gott Brahma sie bei der Erschaffung der Welt gelegt hat, auf einen anderen Stab übertragen werden, wird der Turm zusammen mit dem Tempel zu Staub zerfallen und die Welt wird unter Donnerschlägen untergehen.
Der Prozess erfordert, dass die größere Festplatte niemals auf der kleineren landet. Die Mönche stehen vor einem Dilemma: In welcher Reihenfolge sollen sie die Schichten absolvieren? Es ist erforderlich, ihnen Software zur Berechnung dieser Sequenz zur Verfügung zu stellen.

Unabhängig von Brahma wurde dieses Rätsel Ende des 19. Jahrhunderts vom französischen Mathematiker Edouard Lucas vorgeschlagen. Die verkaufte Version verwendete normalerweise 7-8 Scheiben (Abb. 7).

Reis. 7. Türme von Hanoi-Puzzle.

Angenommen, es gibt eine Lösung für N-1 Festplatte. Dann zum Schalten N Gehen Sie wie folgt vor:

1) Schicht N-1 Festplatte.
2) Schicht N Stecken Sie die Scheibe auf den verbleibenden freien Stift.
3) Wir verschieben den Stapel von N-1 unter Punkt (1) erhaltene Diskette oben N-te Festplatte.

Denn für den Fall N= 1 ist der Umordnungsalgorithmus offensichtlich, dann können wir durch Induktion mit den Aktionen (1) – (3) eine beliebige Anzahl von Scheiben neu anordnen.

Erstellen wir eine rekursive Prozedur, die die gesamte Reihenfolge der Neuanordnungen für eine bestimmte Anzahl von Festplatten ausgibt. Jedes Mal, wenn eine solche Prozedur aufgerufen wird, muss sie Informationen über eine Schicht (ab Punkt 2 des Algorithmus) ausgeben. Bei Neuanordnungen aus den Punkten (1) und (3) ruft sich die Prozedur selbst auf, wobei die Anzahl der Festplatten um eins reduziert wird.

//n – Anzahl der Festplatten //a, b, c – Pin-Nummern. Die Verschiebung erfolgt von Pin a nach Pin b mit Hilfspin c. Prozedur Hanoi(n, a, b, c: ganze Zahl); begin if n > 1 then begin Hanoi(n-1, a, c, b); writeln(a, " -> ", b); Hanoi(n-1, c, b, a); end else writeln(a, " -> ", b); Ende;

Beachten Sie, dass die Menge der rekursiv aufgerufenen Prozeduren in diesem Fall einen Baum bildet, der in umgekehrter Reihenfolge durchlaufen wird.

6.3. Arithmetische Ausdrücke analysieren

Die Aufgabe des Parsens besteht darin, den Wert des Ausdrucks anhand einer vorhandenen Zeichenfolge zu berechnen, die einen arithmetischen Ausdruck und die bekannten Werte der darin enthaltenen Variablen enthält.

Der Prozess der Berechnung arithmetischer Ausdrücke kann als Binärbaum dargestellt werden. Tatsächlich erfordert jeder der arithmetischen Operatoren (+, –, *, /) zwei Operanden, die ebenfalls arithmetische Ausdrücke sind und dementsprechend als Teilbäume betrachtet werden können. Reis. Abbildung 8 zeigt ein Beispiel für einen Baum, der dem Ausdruck entspricht:

Reis. 8. Syntaxbaum entsprechend dem arithmetischen Ausdruck (6).

In einem solchen Baum sind die Endknoten immer Variablen (hier). X) oder numerische Konstanten, und alle internen Knoten enthalten arithmetische Operatoren. Um einen Operator auszuführen, müssen Sie zunächst seine Operanden auswerten. Daher sollte der Baum in der Abbildung in der Endreihenfolge durchlaufen werden. Entsprechende Knotenfolge

angerufen umgekehrte polnische Notation arithmetischer Ausdruck.

Beim Erstellen eines Syntaxbaums sollten Sie die folgende Funktion beachten. Wenn es zum Beispiel einen Ausdruck gibt

und wir lesen die Operationen der Addition und Subtraktion von links nach rechts, dann enthält der korrekte Syntaxbaum ein Minus statt eines Plus (Abb. 9a). Im Wesentlichen entspricht dieser Baum dem Ausdruck. Es ist möglich, die Erstellung eines Baums zu vereinfachen, wenn Sie Ausdruck (8) in umgekehrter Reihenfolge von rechts nach links analysieren. In diesem Fall ist das Ergebnis ein Baum mit Abb. 9b, entspricht Baum 8a, erfordert jedoch keinen Austausch der Schilder.

Ebenso müssen Sie von rechts nach links Ausdrücke analysieren, die Multiplikations- und Divisionsoperatoren enthalten.

Reis. 9. Syntaxbäume für Ausdruck A – B + C beim Lesen von links nach rechts (a) und von rechts nach links (b).

Dieser Ansatz eliminiert die Rekursion nicht vollständig. Es ermöglicht Ihnen jedoch, sich auf nur einen Aufruf einer rekursiven Prozedur zu beschränken, was ausreichend sein kann, wenn das Ziel darin besteht, die Leistung zu maximieren.

7.3. Bestimmen eines Baumknotens anhand seiner Nummer

Die Idee dieses Ansatzes besteht darin, rekursive Aufrufe durch eine einfache Schleife zu ersetzen, die so oft ausgeführt wird, wie Knoten in dem durch die rekursiven Prozeduren gebildeten Baum vorhanden sind. Was bei jedem Schritt genau getan wird, sollte durch die Schrittnummer bestimmt werden. Der Vergleich der Schrittanzahl und der notwendigen Aktionen ist keine triviale Aufgabe und muss jeweils separat gelöst werden.

Nehmen wir zum Beispiel an, Sie möchten etwas tun k verschachtelte Schleifen N Schritte in jedem:

Für i1:= 0 bis n-1 tun, für i2:= 0 bis n-1 tun, für i3:= 0 bis n-1 tun …

Wenn k im Voraus unbekannt ist, ist es unmöglich, sie explizit zu schreiben, wie oben gezeigt. Mit der in Abschnitt 6.5 gezeigten Technik können Sie die erforderliche Anzahl verschachtelter Schleifen mithilfe eines rekursiven Verfahrens erhalten:

Procedure NestedCycles(Indexes: Array of Integer; n, k, Depth: Integer); var i: Ganzzahl; Beginnen Sie mit der Tiefe

Um die Rekursion zu vermeiden und alles auf einen Zyklus zu reduzieren, beachten Sie Folgendes, wenn Sie die Schritte im Basiszahlensystem nummerieren N, dann hat jeder Schritt eine Zahl bestehend aus den Zahlen i1, i2, i3, ... oder den entsprechenden Werten aus dem Indexes-Array. Das heißt, die Zahlen entsprechen den Werten der Zykluszähler. Schrittnummer in regulärer Dezimalschreibweise:

Es wird insgesamt Schritte geben nk. Indem Sie ihre Zahlen im Dezimalzahlensystem durchgehen und jede einzelne davon in das Basiszahlensystem umwandeln N, erhalten wir die Indexwerte:

M:= Round(IntPower(n, k)); for i:= 0 to M-1 do begin Number:= i; for p:= 0 to k-1 do begin Indexes := Number mod n; Zahl:= Zahl div n; Ende;

DoSomething(Indexes); Ende;

Wir weisen noch einmal darauf hin, dass die Methode nicht universell ist und Sie sich für jede Aufgabe etwas anderes einfallen lassen müssen.

Kontrollfragen

1. Bestimmen Sie, was die folgenden rekursiven Prozeduren und Funktionen bewirken.

(a) Was gibt die folgende Prozedur aus, wenn Rec(4) aufgerufen wird?

Prozedur Rec(a: integer); beginne writeln(a); wenn a>0 dann Rec(a-1); writeln(a); Ende;

(b) Welchen Wert hat die Funktion Nod(78, 26)?

Funktion Nod(a, b: integer): integer; begin if a > b then Nod:= Nod(a – b, b) else if b > a then Nod:= Nod(a, b – a) else Nod:= a; Ende;

Prozedur A(n: Ganzzahl); Prozedur B(n: ganze Zahl); Prozedur A(n: ganze Zahl); begin writeln(n); B(n-1); Ende; Prozedur B(n: ganze Zahl); begin writeln(n); wenn n

(d) Was wird die folgende Prozedur ausgeben, wenn BT(0, 1, 3) aufgerufen wird?

Prozedur BT(x: real; D, MaxD: integer); begin if D = MaxD then writeln(x) else begin BT(x – 1, D + 1, MaxD); BT(x + 1, D + 1, MaxD); Ende; Ende; 2. Ouroboros – eine Schlange, die ihren eigenen Schwanz verschlingt (Abb. 14), wenn sie entfaltet ist, hat sie eine Länge L , Durchmesser um den Kopf D , Dicke der Bauchdecke D

. Bestimmen Sie, wie viel Schwanz er in sich hineinquetschen kann und in wie viele Schichten der Schwanz danach gelegt wird?

Reis. 14. Erweiterte Ouroboros.

3. Für den Baum in Abb. 10a zeigt die Reihenfolge der besuchenden Knoten in Vorwärts-, Rückwärts- und Enddurchlaufreihenfolge.

5. Stellen Sie den Syntaxbaum für den folgenden arithmetischen Ausdruck grafisch dar:

Schreiben Sie diesen Ausdruck in umgekehrter polnischer Notation.

6. Notieren Sie für die folgende Grafik (Abb. 15) die Adjazenzmatrix und die Inzidenzmatrix.

Aufgaben

1. Nachdem Sie die Fakultät ausreichend oft (eine Million oder mehr) berechnet haben, vergleichen Sie die Wirksamkeit des rekursiven und des iterativen Algorithmus. Wie oft wird sich die Ausführungszeit unterscheiden und wie hängt dieses Verhältnis von der Zahl ab, deren Fakultät berechnet wird?

2. Schreiben Sie eine rekursive Funktion, die prüft, ob Klammern in einer Zeichenfolge richtig platziert sind. Bei korrekter Anordnung sind folgende Bedingungen erfüllt:

(a) Die Anzahl der öffnenden und schließenden Klammern ist gleich.
(b) In jedem Paar gibt es eine öffnende und schließende Klammer. Die Klammern sind korrekt platziert.

Beispiele für falsche Platzierung:)(, ())(, ())(() usw.

3. Die Zeile darf sowohl runde als auch eckige Klammern enthalten. Zu jeder öffnenden Klammer gehört eine entsprechende schließende Klammer desselben Typs (rund – rund, quadratisch – quadratisch). Schreiben Sie eine rekursive Funktion, die prüft, ob in diesem Fall die Klammern richtig gesetzt sind.

Beispiel für eine falsche Platzierung: ([)].

4. Die Anzahl der regulären Klammerstrukturen der Länge 6 beträgt 5: ()()(), (())(), ()(()), ((())), (()()).
Schreiben Sie ein rekursives Programm, um alle regulären Klammerstrukturen der Länge 2 zu generieren N.

Notiz: Korrekte Klammerstruktur mit minimaler Länge „()“. Strukturen mit längerer Länge werden aus Strukturen mit kürzerer Länge auf zwei Arten erhalten:

(a) wenn die kleinere Struktur in Klammern gesetzt wird,
(b) wenn zwei kleinere Strukturen nacheinander geschrieben werden.

5. Erstellen Sie eine Prozedur, die alle möglichen Permutationen für ganze Zahlen von 1 bis N ausgibt.

6. Erstellen Sie eine Prozedur, die alle Teilmengen der Menge (1, 2, ..., N) druckt.

7. Erstellen Sie eine Prozedur, die alle möglichen Darstellungen der natürlichen Zahl N als Summe anderer natürlicher Zahlen ausgibt.

8. Erstellen Sie eine Funktion, die die Summe der Array-Elemente mithilfe des folgenden Algorithmus berechnet: Das Array wird in zwei Hälften geteilt, die Summen der Elemente in jeder Hälfte werden berechnet und addiert. Die Summe der Elemente in der Hälfte des Arrays wird mit demselben Algorithmus berechnet, also wiederum durch Halbierung. Divisionen finden so lange statt, bis die resultierenden Teile des Arrays jeweils ein Element enthalten und die Berechnung der Summe dementsprechend trivial wird.

Kommentar: Dieser Algorithmus ist eine Alternative. Bei Arrays mit reellen Werten sind normalerweise kleinere Rundungsfehler möglich.

10. Erstellen Sie eine Prozedur, die die Koch-Kurve zeichnet (Abbildung 12).

11. Reproduzieren Sie die Figur. 16. In der Abbildung ist der Kreis bei jeder nächsten Iteration 2,5-mal kleiner (dieser Koeffizient kann als Parameter verwendet werden).

Literatur

1. D. Knuth. Die Kunst der Computerprogrammierung. v. 1. (Abschnitt 2.3. „Bäume“).
2. N. Wirth. Algorithmen und Datenstrukturen.